Regresión lineal simple (2/4)
Gonzalo Pérez
10 de febrero de 2020
Ejemplo de motivación.
Supongamos que nos realizan una consulta sobre cómo promover las ventas de determinado producto. Consideremos los siguientes datos que incluyen el total de ventas de ese producto (sales, en miles de unidades) en 200 diferentes mercados, junto con los gastos (en miles de dólares) realizados en publicidad en los tres siguientes medios: TV, radio y periódico (newspaper).
library(ISLR)
Datos=read.csv("images/archivos/Advertising.csv", header=TRUE, sep="," )
head(Datos)## X TV radio newspaper sales
## 1 1 230.1 38 69 22.1
## 2 2 44.5 39 45 10.4
## 3 3 17.2 46 69 9.3
## 4 4 151.5 41 58 18.5
## 5 5 180.8 11 58 12.9
## 6 6 8.7 49 75 7.2str(Datos)## 'data.frame': 200 obs. of 5 variables:
## $ X : int 1 2 3 4 5 6 7 8 9 10 ...
## $ TV : num 230.1 44.5 17.2 151.5 180.8 ...
## $ radio : num 37.8 39.3 45.9 41.3 10.8 48.9 32.8 19.6 2.1 2.6 ...
## $ newspaper: num 69.2 45.1 69.3 58.5 58.4 75 23.5 11.6 1 21.2 ...
## $ sales : num 22.1 10.4 9.3 18.5 12.9 7.2 11.8 13.2 4.8 10.6 ...El gasto en publicidad en televisión (TV) es una variable que se puede controlar, de manera que a partir de ésta se podría analizar si a mayor gasto en publicidad en TV hay mayores ventas. En caso afirmativo podríamos sugerir aumentar el gasto en publicidad en TV, en caso contrario podríamos sugerir realizar el gasto en otro tipo de publicidad. Veamos como se ven los datos.
- \(Y\)- Total de ventas del producto (sales).
- \(X\)- Total de gasto en publicidad en TV (TV).
Modelo de regresión lineal simple.
En el modelo de regresión lineal simple se asume lo siguiente:
\[y_i=\alpha+\beta x_i + \epsilon_i, i=1,..., n,\]
donde \(E(\epsilon_i)=0, \; V(\epsilon_i)=\sigma^2 \;\; \text{y} \;\; Cov(\epsilon_i, \epsilon_j)=0, \; i\neq j \; \; \forall i,j = 1,...,n.\)
En general, se realiza el supuesto adicional siguiente para realizar inferencias sobre los parámetros:
\[y_i \sim N(\mu_i, \sigma^2),\] con \(\mu_i=\alpha+\beta x_i\); \(y_i\) y \(y_j\) variables independientes para \(\; i\neq j \; \; \forall i,j = 1,...,n.\)
Estimaciones para combinaciones lineales de los parámetros.
En la clase pasada observamos que los estimadores de \(\alpha\) y \(\beta\) son:
\[\begin{align} \widehat{\alpha} = \overline{y} - \widehat{\beta}\overline{x} \end{align}\]
\[\begin{align} \widehat{\beta} = \frac{\sum_{i=1}^{n}(x_{i}-\overline{x})(y_{i}-\overline{y})}{\sum_{i=1}^{n}(x_{i}-\overline{x})^2} \end{align}\]
En general hay dos usos de la regresión:
- Describir un fenómeno (en general, en promedio).
- Predecir (nuevas observaciones).
Hay más incertidumbre cuando se predice que cuando se describe un fenómeno en general.
Descripción del fenómeno
En este caso nos interesa realizar inferencias sobre aspectos relacionados con combinaciones lineales de los parámetros. Por ejemplo:
Inferencias sobre los parámetros. Aquí la idea fue describir, por ejemplo, el cambio que en general se espera en la variable \(Y\) cuando se aumenta en una unidad la variable \(X\).
Otro aspecto a considerar es \(E(Y|X=x)=\alpha+\beta x\). Es decir, cual sería el valor esperado o el promedio que se espera cuando el valor de la variable independiente es \(X=x\).
En general, supongamos que se tiene interés en estimar
\[\theta=z_0 \alpha + z_1 \beta,\] donde \(z_0\) y \(z_1\) son constantes, no ambas iguales a cero.
Consideremos \(\widehat{\theta}=z_0 \widehat{\alpha} + z_1 \widehat{\beta}\). Las propiedades siguientes se cumplen:
- De acuerdo con el Teorema de Gauss-Markov, el estimador \(z_0 \widehat{\alpha} + z_1 \widehat{\beta}\) es el de mínima varianza entre los estimadores lineales e insesgados.
- \(E(\widehat{\theta})=E(z_0 \widehat{\alpha} + z_1 \widehat{\beta})=\theta=z_0 \alpha + z_1 \beta\)
- \(V(\widehat{\theta})=V(z_0 \widehat{\alpha} + z_1 \widehat{\beta})=\sigma^2[\dfrac{z_0^2}{n}+\dfrac{(z_1-z_0\overline{x})^2}{\sum_{i=1}^{n}(x_{i}-\overline{x})^2} ]\)
- \(z_0 \widehat{\alpha} + z_1 \widehat{\beta} \sim N(z_0 \alpha + z_1 \beta, \sigma^2[\dfrac{z_0^2}{n}+\dfrac{(z_1-z_0\overline{x})^2}{\sum_{i=1}^{n}(x_{i}-\overline{x})^2} )\)
- Un estimador insesgado de \(V(\widehat{\theta})\) es \(\hat{V}(\widehat{\theta})= \widehat{Var}(z_0 \widehat{\alpha} + z_1 \widehat{\beta})=\hat{\sigma}^2[\dfrac{z_0^2}{n}+\dfrac{(z_1-z_0\overline{x})^2}{\sum_{i=1}^{n}(x_{i}-\overline{x})^2} ]\)
- Un intervalo de confianza para \(\theta\) es \[[\hat{\theta} - t_{n-2, 1-\frac{\delta}{2}}\sqrt{ \widehat{Var}(\hat{\theta})}, \; \hat{\theta} + t_{n-2, 1-\frac{\delta}{2}}\sqrt{ \widehat{Var}(\hat{\theta})}] \]
- Considerando la siguiente prueba de hipótesis \[H_0: z_0 \alpha + z_1 \beta = c_0 \] vs \[H_a: z_0 \alpha + z_1 \beta \neq c_0 \] La estadística de prueba es \[t^*= \dfrac{z_0 \widehat{\alpha} + z_1 \widehat{\beta} -c_0}{\sqrt{ \widehat{Var}(z_0 \widehat{\alpha} + z_1 \widehat{\beta})}}\] La regla de decisión para una significancia \(\delta\) es: Rechazar \(H_0\) si \(|t^*|> t_{n-2, 1-\frac{\delta}{2}}\).
Casos particulares son:
- \(E(Y|X=x)=\alpha+\beta x\), donde \(z_0=1\) y \(z_1=x\).
- \(E(Y|X=x+z_1)-E(Y|X=x)= \alpha+(x+z_1)\beta-(\alpha+x\beta)=z_1\beta\), donde \(z_0=0\).
- \(E(Y|X=0)=\alpha\), donde \(z_0=1\) y \(z_1=0\).
En R, se pueden obtener los intervalos de confianza para \(E(Y|X=x)\) de forma muy sencilla usando la función predict().
fit1=lm(sales~TV, data=Datos)
newdata <- data.frame(TV = seq(min(Datos$TV), max(Datos$TV), 5))
pred.w.clim <- predict(fit1, newdata, interval = "confidence", level = 0.95)
options(digits=10)
head(pred.w.clim)## fit lwr upr
## 1 7.065869197 6.166202463 7.965535932
## 2 7.303552400 6.426680406 8.180424393
## 3 7.541235602 6.686942681 8.395528523
## 4 7.778918804 6.946971727 8.610865880
## 5 8.016602006 7.206748239 8.826455773
## 6 8.254285208 7.466250977 9.042319440matplot(newdata$TV, cbind(pred.w.clim),
lty = c(1,2,2), type = "l", ylab = "Estimation of E(sales|TV)", xlab = "TV")
points(Datos$TV, Datos$sales, cex=.5)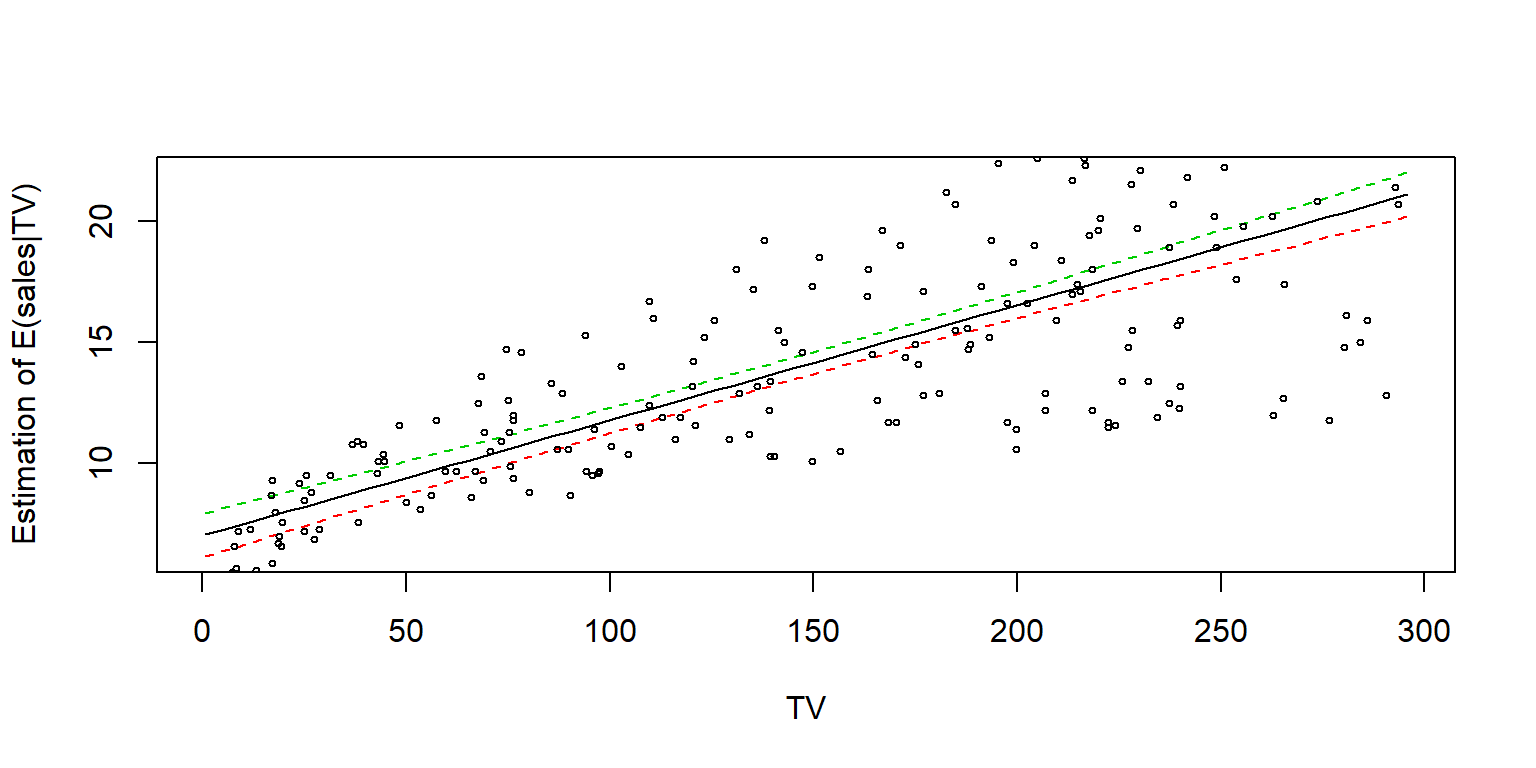
También se pueden hacer los cálculos a mano
delta=.05
ttab=qt(1-delta/2, n-2,lower.tail = TRUE)
x=min(Datos$TV)
yfit=alpha+beta*x
Var.yfit=SSE*(1/n+(x-xbar)^2/SSx)
print(c(yfit-ttab*sqrt(Var.yfit),
yfit+ttab*sqrt(Var.yfit)))## [1] 6.166202463 7.965535932O usar la función asociada a pruebas de hipótesis del modelo lineal general usando matrices. Esta prueba es más general y sirve para cualquier valor de \(z_0\) y \(z_1\).
library(multcomp)
#Para alpha
K=matrix(c(1,0), ncol=2, nrow=1)
m=0
prueba1=glht(fit1, linfct=K, rhs=m)
confint(prueba1)##
## Simultaneous Confidence Intervals
##
## Fit: lm(formula = sales ~ TV, data = Datos)
##
## Quantile = 1.9720175
## 95% family-wise confidence level
##
##
## Linear Hypotheses:
## Estimate lwr upr
## 1 == 0 7.0325935 6.1297193 7.9354678#Para beta
K=matrix(c(0,1), ncol=2, nrow=1)
m=0
prueba2=glht(fit1, linfct=K, rhs=m)
confint(prueba2)##
## Simultaneous Confidence Intervals
##
## Fit: lm(formula = sales ~ TV, data = Datos)
##
## Quantile = 1.9720175
## 95% family-wise confidence level
##
##
## Linear Hypotheses:
## Estimate lwr upr
## 1 == 0 0.04753664 0.04223072 0.05284256#Para E(Y|X), con X el mínimo valor observado en los datos
K=matrix(c(1,min(Datos$TV)), ncol=2, nrow=1)
m=0
prueba3=glht(fit1, linfct=K, rhs=m)
confint(prueba3)##
## Simultaneous Confidence Intervals
##
## Fit: lm(formula = sales ~ TV, data = Datos)
##
## Quantile = 1.9720175
## 95% family-wise confidence level
##
##
## Linear Hypotheses:
## Estimate lwr upr
## 1 == 0 7.0658692 6.1662025 7.9655359Además la función glht permite hacer pruebas de hipótesis. Por ejemplo repetiremos la prueba de la sesión pasada
\[H_0: \beta \leq 1 \] vs \[H_a: \beta > 1 \]
#Para beta
K=matrix(c(0,1), ncol=2, nrow=1)
m=1
summary(glht(fit1, linfct=K, rhs=m, alternative="greater"))##
## Simultaneous Tests for General Linear Hypotheses
##
## Fit: lm(formula = sales ~ TV, data = Datos)
##
## Linear Hypotheses:
## Estimate Std. Error t value Pr(>t)
## 1 <= 1 0.047536640 0.002690607 -353.9957 1
## (Adjusted p values reported -- single-step method)Por default se realiza la prueba
\[H_0: \beta = 1 \] vs \[H_a: \beta \neq 1 \]
Lo que se modifica es la forma de calcular el p-value
#Para beta
K=matrix(c(0,1), ncol=2, nrow=1)
m=1
summary(glht(fit1, linfct=K, rhs=m))##
## Simultaneous Tests for General Linear Hypotheses
##
## Fit: lm(formula = sales ~ TV, data = Datos)
##
## Linear Hypotheses:
## Estimate Std. Error t value Pr(>|t|)
## 1 == 1 0.047536640 0.002690607 -353.9957 < 2.22e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## (Adjusted p values reported -- single-step method)Hagamos una prueba donde la variable independiente es newspaper. Así podremos comprobar la equivalencia en el cálculo de los p-values.
#Para beta
fit1=lm(sales~newspaper, data=Datos)
K=matrix(c(0,1), ncol=2, nrow=1)
m=0
#Pruebas simultaneas (sólo hay una, así que debe coincidir con la global)
summary(glht(fit1, linfct=K, rhs=m))##
## Simultaneous Tests for General Linear Hypotheses
##
## Fit: lm(formula = sales ~ newspaper, data = Datos)
##
## Linear Hypotheses:
## Estimate Std. Error t value Pr(>|t|)
## 1 == 0 0.05469310 0.01657572 3.29959 0.0011482 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## (Adjusted p values reported -- single-step method)#Prueba global
summary(glht(fit1, linfct=K, rhs=m),test=Ftest())##
## General Linear Hypotheses
##
## Linear Hypotheses:
## Estimate
## 1 == 0 0.0546931
##
## Global Test:
## F DF1 DF2 Pr(>F)
## 1 10.8873 1 198 0.001148196#La prueba de la tabla anova coincide en este caso con la prueba global y con la individual
summary(fit1)##
## Call:
## lm(formula = sales ~ newspaper, data = Datos)
##
## Residuals:
## Min 1Q Median 3Q Max
## -11.2272370 -3.3873039 -0.8392027 3.5059132 12.7751274
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 12.35140707 0.62142019 19.87610 < 2.22e-16 ***
## newspaper 0.05469310 0.01657572 3.29959 0.0011482 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 5.09248 on 198 degrees of freedom
## Multiple R-squared: 0.05212045, Adjusted R-squared: 0.04733317
## F-statistic: 10.8873 on 1 and 198 DF, p-value: 0.001148196#Resultafo de la prueba de la tabla anova.
anova(fit1)## Analysis of Variance Table
##
## Response: sales
## Df Sum Sq Mean Sq F value Pr(>F)
## newspaper 1 282.3442 282.344206 10.8873 0.0011482 **
## Residuals 198 5134.8045 25.933356
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1### La siguiente no es equivalente, recae en supuestos asintóticos
summary(glht(fit1, linfct=K, rhs=m),test=Chisqtest())##
## General Linear Hypotheses
##
## Linear Hypotheses:
## Estimate
## 1 == 0 0.0546931
##
## Global Test:
## Chisq DF Pr(>Chisq)
## 1 10.8873 1 0.0009682592Otra forma de hacer algunas pruebas de hipótesis es usando la función anova(). Para esto es necesario ajustar dos modelos, el completo o sin restrincciones y uno restringido.
Por ejemplo, para la prueba \[H_0: \beta = 1 \] vs \[H_a: \beta \neq 1 \]
fit1=lm(sales~TV, data=Datos)
fit2=lm(sales~offset(TV), data=Datos)
anova(fit1, fit2)## Analysis of Variance Table
##
## Model 1: sales ~ TV
## Model 2: sales ~ offset(TV)
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 198 2102.53
## 2 199 1332780.88 -1 -1330678.4 125312.95 < 2.22e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1