Regresión lineal simple (2a/4)
Gonzalo Pérez
24 de febrero de 2020
Ejemplo de motivación.
Supongamos que nos realizan una consulta sobre cómo promover las ventas de determinado producto. Consideremos los siguientes datos que incluyen el total de ventas de ese producto (sales, en miles de unidades) en 200 diferentes mercados, junto con los gastos (en miles de dólares) realizados en publicidad en los tres siguientes medios: TV, radio y periódico (newspaper).
library(ISLR)
Datos=read.csv("images/archivos/Advertising.csv", header=TRUE, sep="," )
head(Datos)## X TV radio newspaper sales
## 1 1 230.1 38 69 22.1
## 2 2 44.5 39 45 10.4
## 3 3 17.2 46 69 9.3
## 4 4 151.5 41 58 18.5
## 5 5 180.8 11 58 12.9
## 6 6 8.7 49 75 7.2str(Datos)## 'data.frame': 200 obs. of 5 variables:
## $ X : int 1 2 3 4 5 6 7 8 9 10 ...
## $ TV : num 230.1 44.5 17.2 151.5 180.8 ...
## $ radio : num 37.8 39.3 45.9 41.3 10.8 48.9 32.8 19.6 2.1 2.6 ...
## $ newspaper: num 69.2 45.1 69.3 58.5 58.4 75 23.5 11.6 1 21.2 ...
## $ sales : num 22.1 10.4 9.3 18.5 12.9 7.2 11.8 13.2 4.8 10.6 ...El gasto en publicidad en televisión (TV) es una variable que se puede controlar, de manera que a partir de ésta se podría analizar si a mayor gasto en publicidad en TV hay mayores ventas. En caso afirmativo podríamos sugerir aumentar el gasto en publicidad en TV, en caso contrario podríamos sugerir realizar el gasto en otro tipo de publicidad. Veamos como se ven los datos.
- \(Y\)- Total de ventas del producto (sales).
- \(X\)- Total de gasto en publicidad en TV (TV).
Modelo de regresión lineal simple.
En el modelo de regresión lineal simple se asume lo siguiente:
\[y_i=\alpha+\beta x_i + \epsilon_i, i=1,..., n,\]
donde \(E(\epsilon_i)=0, \; V(\epsilon_i)=\sigma^2 \;\; \text{y} \;\; Cov(\epsilon_i, \epsilon_j)=0, \; i\neq j \; \; \forall i,j = 1,...,n.\)
En general, se realiza el supuesto adicional siguiente para realizar inferencias sobre los parámetros:
\[y_i \sim N(\mu_i, \sigma^2),\] con \(\mu_i=\alpha+\beta x_i\); \(y_i\) y \(y_j\) variables independientes para \(\; i\neq j \; \; \forall i,j = 1,...,n.\)
Predicción.
Recordemos que si \(\widehat{\theta}=z_0 \widehat{\alpha} + z_1 \widehat{\beta}\), donde \(z_0\) y \(z_1\) son constantes, no ambas iguales a cero. Entonces \(\hat{V}(\widehat{\theta})= \widehat{Var}(z_0 \widehat{\alpha} + z_1 \widehat{\beta})=\hat{\sigma}^2[\dfrac{z_0^2}{n}+\dfrac{(z_1-z_0\overline{x})^2}{\sum_{i=1}^{n}(x_{i}-\overline{x})^2} ]\).
Un intervalo de confianza para \(\theta=z_0 \alpha + z_1 \beta\) es \[[\hat{\theta} - t_{n-2, 1-\frac{\delta}{2}}\sqrt{ \widehat{Var}(\hat{\theta})}, \; \hat{\theta} + t_{n-2, 1-\frac{\delta}{2}}\sqrt{ \widehat{Var}(\hat{\theta})}] \] Casos particulares
- \(E(Y|X=x)=\alpha+\beta x\), donde \(z_0=1\) y \(z_1=x\).
- \(E(Y|X=x+z_1)-E(Y|X=x)= \alpha+(x+z_1)\beta-(\alpha+x\beta)=z_1\beta\), donde \(z_0=0\).
- \(E(Y|X=0)=\alpha\), donde \(z_0=1\) y \(z_1=0\).
Ahora analizaremos el caso de predicción. Donde el objetivo es decir algo sobre futuros valores de variables aleatorias \(y_{h1},..., y_{hm}\) de las cuales sólo se conoce el valor \(x_{h1},..., x_{hm}\). Estas observaciones \(y_{h1},..., y_{hm}\) se asumen independientes de las usadas para ajustar el modelo, es decir, de las \(y_1,..., y_n\), aunque siguen el modelo:
\[y_{hi} \sim N(\mu_{hi}, \sigma^2),\] con \(\mu_{hi}=\alpha+\beta x_{hi}\); \(y_{hi}\) y \(y_{hj}\) variables independientes para \(\; i\neq j \; \; \forall i,j = 1,...,m\), e independientes de \(y_1,..., y_n\).
En R, se pueden obtener los intervalos de predicción para el valor de una nueva observación \(y_h\) donde se conoce \(x_h\) usando la función predict(). Es decir, se puede obtener el intervalo de predicción siguiente:
\[[\hat{\theta} - t_{n-2, 1-\frac{\delta}{2}}\sqrt{ \hat{\sigma}^2[1+\dfrac{1}{n}+\dfrac{(x_h-\overline{x})^2}{\sum_{i=1}^{n}(x_{i}-\overline{x})^2} ]}, \; \hat{\theta} + t_{n-2, 1-\frac{\delta}{2}}\sqrt{ \hat{\sigma}^2[1+\dfrac{1}{n}+\dfrac{(x_h-\overline{x})^2}{\sum_{i=1}^{n}(x_{i}-\overline{x})^2} ]}] \]
fit1=lm(sales~TV, data=Datos)
newdata <- data.frame(TV = seq(min(Datos$TV), max(Datos$TV), 5))
pred.w.clim <- predict(fit1, newdata, interval = "prediction", level = 0.95)
options(digits=10)
head(pred.w.clim)## fit lwr upr
## 1 7.065869197 0.5770701962 13.55466820
## 2 7.303552400 0.8178745831 13.78923022
## 3 7.541235602 1.0585719023 14.02389930
## 4 7.778918804 1.2991620042 14.25867560
## 5 8.016602006 1.5396447444 14.49355927
## 6 8.254285208 1.7800199838 14.72855043matplot(newdata$TV, cbind(pred.w.clim),
lty = c(1,2,2), type = "l", ylab = "Nuevas ventas dado un gasto de TV", xlab = "TV")
points(Datos$TV, Datos$sales, cex=.5)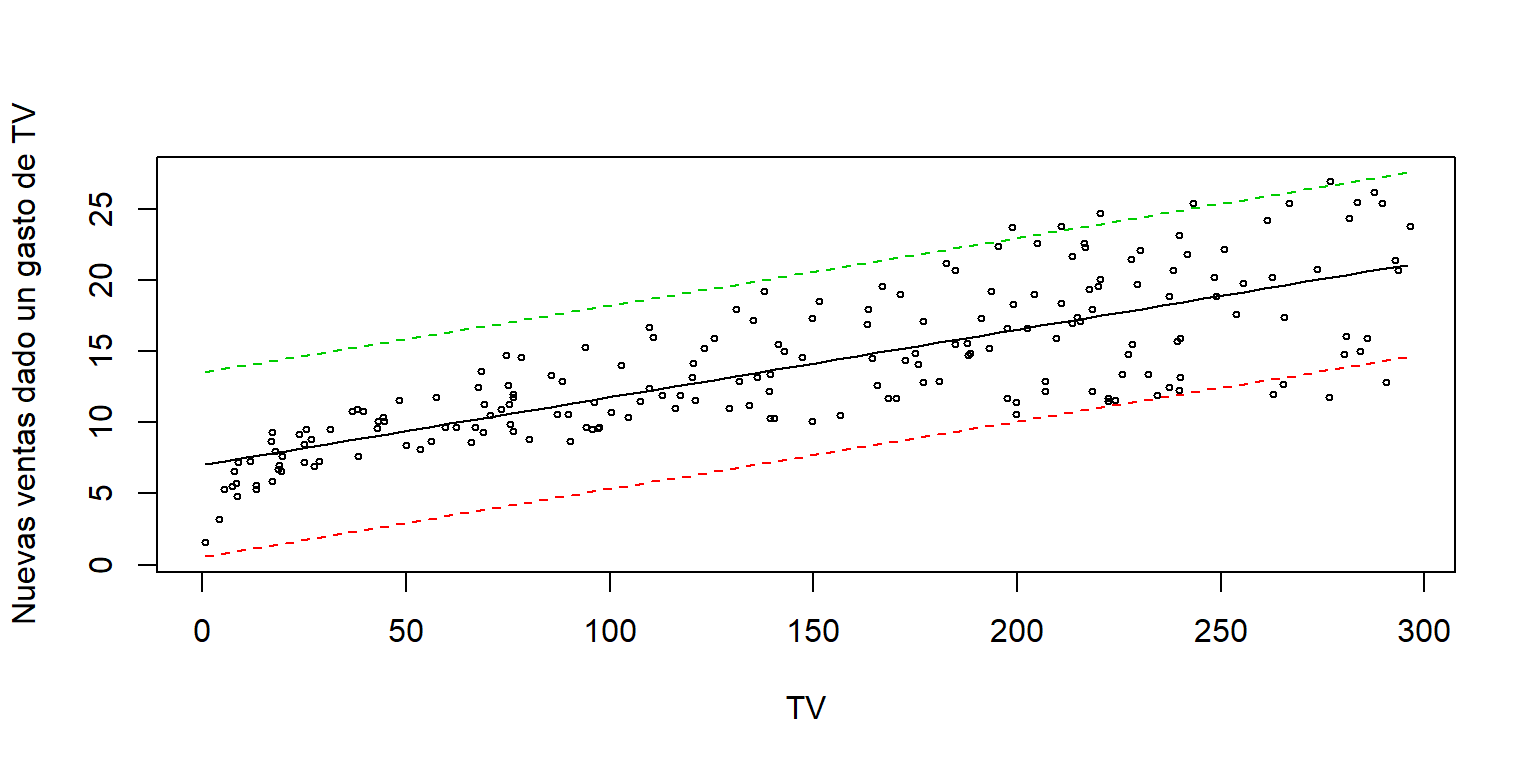
También se pueden hacer los cálculos a mano
delta=.05
ttab=qt(1-delta/2, n-2,lower.tail = TRUE)
x=min(Datos$TV)
yfit=alpha+beta*x
Var.yfit=SSE*(1/n+(x-xbar)^2/SSx)
Var.yfitpred=SSE*(1+1/n+(x-xbar)^2/SSx)
print(c(yfit-ttab*sqrt(Var.yfit),
yfit+ttab*sqrt(Var.yfit)))## [1] 6.166202463 7.965535932print(c(yfit-ttab*sqrt(Var.yfitpred),
yfit+ttab*sqrt(Var.yfitpred)))## [1] 0.5770701962 13.5546681987Nota: el paquete investr también se puede usar para intervalos de predicción. Este paquete se usará también para intervalos simultáneos y problemas de calibración.
library(investr)
pred.w.clim2=predFit(fit1, newdata, interval = "prediction", level = 0.95, adjust = c("none"))
head(pred.w.clim2)## fit lwr upr
## 1 7.065869197 0.5770701962 13.55466820
## 2 7.303552400 0.8178745831 13.78923022
## 3 7.541235602 1.0585719023 14.02389930
## 4 7.778918804 1.2991620042 14.25867560
## 5 8.016602006 1.5396447444 14.49355927
## 6 8.254285208 1.7800199838 14.72855043Sin embargo, para el promedio de nuevas observaciones o para el total no necesariamente. En ese caso se podrían usar los resultados que se obtienen a partir de las pruebas de hipótesis general que sirve para cualquier valor de \(z_0\) y \(z_1\) (no ambos igual a cero). En particular, dado que de ahí se obtienen las varianzas de estimadores que son combinaciones lineales.
Por ejemplo. Supongamos que deseamos saber cuál sería el total de ventas para tres mercados en donde se realizarán los siguientes gastos en publicidad:
(xh1=min(Datos$TV))## [1] 0.7(xh2=mean(Datos$TV))## [1] 147.0425(xh3=max(Datos$TV))## [1] 296.4Primero a mano:
delta=.05
ttab=qt(1-delta/2, n-2,lower.tail = TRUE)
m=3
sumxhs=(xh1+xh2+xh3)
totalpred=(alpha*m+beta*sumxhs)
Var.totalpred=SSE*(m+m^2/n+(sumxhs-m*xbar)^2/SSx)
print(c(totalpred-ttab*sqrt(Var.totalpred),
totalpred+ttab*sqrt(Var.totalpred)))## [1] 30.99726543 53.42438051El paquete multcomp sirve para calcular intervalos de confianza, no de predicción, así que se deben ajustar.
library(multcomp)
#Para alpha
K=matrix(c(m,sumxhs), ncol=2, nrow=1)
m2=0
prueba1=glht(fit1, linfct=K, rhs=m2)
###intervalo del promedio esperado del total dado los valores de gastos en TV
confint(prueba1)##
## Simultaneous Confidence Intervals
##
## Fit: lm(formula = sales ~ TV, data = Datos)
##
## Quantile = 1.9720175
## 95% family-wise confidence level
##
##
## Linear Hypotheses:
## Estimate lwr upr
## 1 == 0 42.2108230 40.8475416 43.5741043Prueba1=summary(prueba1)
Prueba1 ##
## Simultaneous Tests for General Linear Hypotheses
##
## Fit: lm(formula = sales ~ TV, data = Datos)
##
## Linear Hypotheses:
## Estimate Std. Error t value Pr(>|t|)
## 1 == 0 42.210823 0.691313 61.05892 < 2.22e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## (Adjusted p values reported -- single-step method)###Valor de la suma predicha
Prueba1[[9]]$coefficients## 1
## 42.21082297###Parte de la varianza
Prueba1[[9]]$sigma## 1
## 0.6913130024###El valor de sigma estimada del modelo.
summary(fit1)$sigma## [1] 3.258656369##Modificación a la varianza
Var.totalpred2=summary(fit1)$sigma^2*m+ (Prueba1[[9]]$sigma)^2
Var.totalpred2## 1
## 32.33443765Var.totalpred## [1] 32.33443765