Regresión lineal simple (2b/4)
Gonzalo Pérez
25 de febrero de 2020
Ejemplo de motivación.
Supongamos que nos realizan una consulta sobre cómo promover las ventas de determinado producto. Consideremos los siguientes datos que incluyen el total de ventas de ese producto (sales, en miles de unidades) en 200 diferentes mercados, junto con los gastos (en miles de dólares) realizados en publicidad en los tres siguientes medios: TV, radio y periódico (newspaper).
library(ISLR)
Datos=read.csv("images/archivos/Advertising.csv", header=TRUE, sep="," )
head(Datos)## X TV radio newspaper sales
## 1 1 230.1 38 69 22.1
## 2 2 44.5 39 45 10.4
## 3 3 17.2 46 69 9.3
## 4 4 151.5 41 58 18.5
## 5 5 180.8 11 58 12.9
## 6 6 8.7 49 75 7.2str(Datos)## 'data.frame': 200 obs. of 5 variables:
## $ X : int 1 2 3 4 5 6 7 8 9 10 ...
## $ TV : num 230.1 44.5 17.2 151.5 180.8 ...
## $ radio : num 37.8 39.3 45.9 41.3 10.8 48.9 32.8 19.6 2.1 2.6 ...
## $ newspaper: num 69.2 45.1 69.3 58.5 58.4 75 23.5 11.6 1 21.2 ...
## $ sales : num 22.1 10.4 9.3 18.5 12.9 7.2 11.8 13.2 4.8 10.6 ...El gasto en publicidad en televisión (TV) es una variable que se puede controlar, de manera que a partir de ésta se podría analizar si a mayor gasto en publicidad en TV hay mayores ventas. En caso afirmativo podríamos sugerir aumentar el gasto en publicidad en TV, en caso contrario podríamos sugerir realizar el gasto en otro tipo de publicidad. Veamos como se ven los datos.
- \(Y\)- Total de ventas del producto (sales).
- \(X\)- Total de gasto en publicidad en TV (TV).
Modelo de regresión lineal simple.
En el modelo de regresión lineal simple se asume lo siguiente:
\[y_i=\alpha+\beta x_i + \epsilon_i, i=1,..., n,\]
donde \(E(\epsilon_i)=0, \; V(\epsilon_i)=\sigma^2 \;\; \text{y} \;\; Cov(\epsilon_i, \epsilon_j)=0, \; i\neq j \; \; \forall i,j = 1,...,n.\)
En general, se realiza el supuesto adicional siguiente para realizar inferencias sobre los parámetros:
\[y_i \sim N(\mu_i, \sigma^2),\] con \(\mu_i=\alpha+\beta x_i\); \(y_i\) y \(y_j\) variables independientes para \(\; i\neq j \; \; \forall i,j = 1,...,n.\)
Intervalos simultáneos
En ocasiones nos interesa proporcionar intervalos de confianza o de predicción de forma simultánea. Por ejemplo, se tiene interés en saber cuáles serían las ventas en dos mercados A y B con gastos en publicidad \(x_{h1}\) y \(x_{h2}\). Es decir, para cada mercado nos interesa saber sus ventas de forma simultánea y no sólo el total de ventas en ambos mercados.
Todos los intervalos anteriores se desarrollaron para un parámetro en particular \(\theta\) o bien una función unidimensional de nuevas observaciones \(y_{h1},..., y_{hk}\).
Existen tres métodos comúnmente usados para calcular intervalos de confianza/predicción simultáneos.
Método de Bonferroni Supongamos que se tiene interés en k predicciones o bien k intervalos de confianza, entonces se calculan los intervalos tal como se han visto pero en lugar de usar el valor de \(t_{n-2, 1-\frac{\delta}{2}}\) se usan los de \(t_{n-2, 1-\frac{\delta}{2k}}\).
Método de Scheffé
- k intervalos de confianza
Se calculan los intervalos tal como se han visto pero en lugar de usar el valor de \(t_{n-2, 1-\frac{\delta}{2}}\) se usan los de \((2 {F}_{2 , n-2 , 1-\delta})^{1/2}\).
- k intervalos de predicción
Se calculan los intervalos tal como se han visto pero en lugar de usar el valor de \(t_{n-2, 1-\frac{\delta}{2}}\) se usan los de \((k {F}_{k , n-2 , 1-\delta})^{1/2}\).
Método del máximo módulo
Se calculan los intervalos tal como se han visto pero en lugar de usar el valor de \(t_{n-2, 1-\frac{\delta}{2}}\) se usan los de \(u_{k,n-2, 1-\delta}\).
fit1=lm(sales~TV, data=Datos)
summary(fit1)##
## Call:
## lm(formula = sales ~ TV, data = Datos)
##
## Residuals:
## Min 1Q Median 3Q Max
## -8.386 -1.955 -0.191 2.067 7.212
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 7.03259 0.45784 15.4 <2e-16 ***
## TV 0.04754 0.00269 17.7 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 3.3 on 198 degrees of freedom
## Multiple R-squared: 0.612, Adjusted R-squared: 0.61
## F-statistic: 312 on 1 and 198 DF, p-value: <2e-16Por ejemplo. Supongamos que deseamos saber las ventas para tres mercados en donde se realizarán los siguientes gastos en publicidad:
(xh1=min(Datos$TV))## [1] 0.7(xh2=mean(Datos$TV))## [1] 147(xh3=max(Datos$TV))## [1] 296Estamos hablando de predicción. Entonces, la función predict() nos podría dar los intervalos de Bonferroni, pero deberíamos ajustar el nivel.
newdata <- data.frame(TV = c(xh1, xh2, xh3))
delta=.05
level1= 1-delta/length(newdata$TV)
pred.w.clim <- predict(fit1, newdata, interval = "prediction", level = level1)
options(digits=10)
head(pred.w.clim)## fit lwr upr
## 1 7.065869197 -0.8788634712 15.01060187
## 2 14.022500000 6.1348555990 21.91014440
## 3 21.122453773 13.1753534593 29.06955409Se pueden hacer los cálculos a mano. Por ejemplo, uno de esos intervalos de predicción.
delta=.05
ttab=qt(1-delta/(2*length(newdata$TV)), n-2,lower.tail = TRUE)
yfith=alpha+beta*xh1
Var.yfithpred=SSE*(1+1/n+(xh1-xbar)^2/SSx)
print(c(yfith-ttab*sqrt(Var.yfithpred),
yfith+ttab*sqrt(Var.yfithpred)))## [1] -0.8788634712 15.0106018660El paquete investr también se puede usar para intervalos de predicción/confianza simultáneos.
library(investr)
pred.w.clim2=predFit(fit1, newdata, interval = "prediction", level = 0.95, adjust = c("Bonferroni"), k=length(newdata$TV))
head(pred.w.clim2)## fit lwr upr
## 1 7.065869197 -0.8788634712 15.01060187
## 2 14.022500000 6.1348555990 21.91014440
## 3 21.122453773 13.1753534593 29.06955409También se pueden obtener los intervalos por el método de Scheffé, por ejemplo.
library(investr)
pred.w.climScheffe=predFit(fit1, newdata, interval = "prediction", level = 0.95, adjust = c("Scheffe"), k=length(newdata$TV))
head(pred.w.climScheffe)## fit lwr upr
## 1 7.065869197 -2.212128932 16.34386733
## 2 14.022500000 4.811170550 23.23382945
## 3 21.122453773 11.841690666 30.40321688A mano, uno de los intervalos de Scheffé
delta=.05
Ftab=qf(1-delta,length(newdata$TV) ,n-2,lower.tail = TRUE)
yfith=alpha+beta*xh1
Var.yfithpred=SSE*(1+1/n+(xh1-xbar)^2/SSx)
print(c(yfith-sqrt(length(newdata$TV)*Ftab)*sqrt(Var.yfithpred),
yfith+sqrt(length(newdata$TV)*Ftab)*sqrt(Var.yfithpred)))## [1] -2.212128932 16.343867327En general, la banda de intervalos simultáneos llamada Working-Hotelling band se puede graficar como sigue (sólo es de confianza!).
plotFit(fit1, interval = "confidence", adjust = "Scheffe")
Comparación con los intervalos de confianza individuales:
fit1=lm(sales~TV, data=Datos)
newdata <- data.frame(TV = seq(min(Datos$TV), max(Datos$TV), 5))
pred.w.clim <- predict(fit1, newdata, interval = "confidence", level = 0.95)
pred.w.climScheffe=predFit(fit1, newdata, interval = "confidence", level = 0.95, adjust = c("Scheffe"))
matplot(newdata$TV, cbind(pred.w.clim, pred.w.climScheffe[,2:3]),
lty = c(1,2,2, 1, 1), type = "l", ylab = "Nuevas ventas dado un gasto de TV", xlab = "TV")
points(Datos$TV, Datos$sales, cex=.5)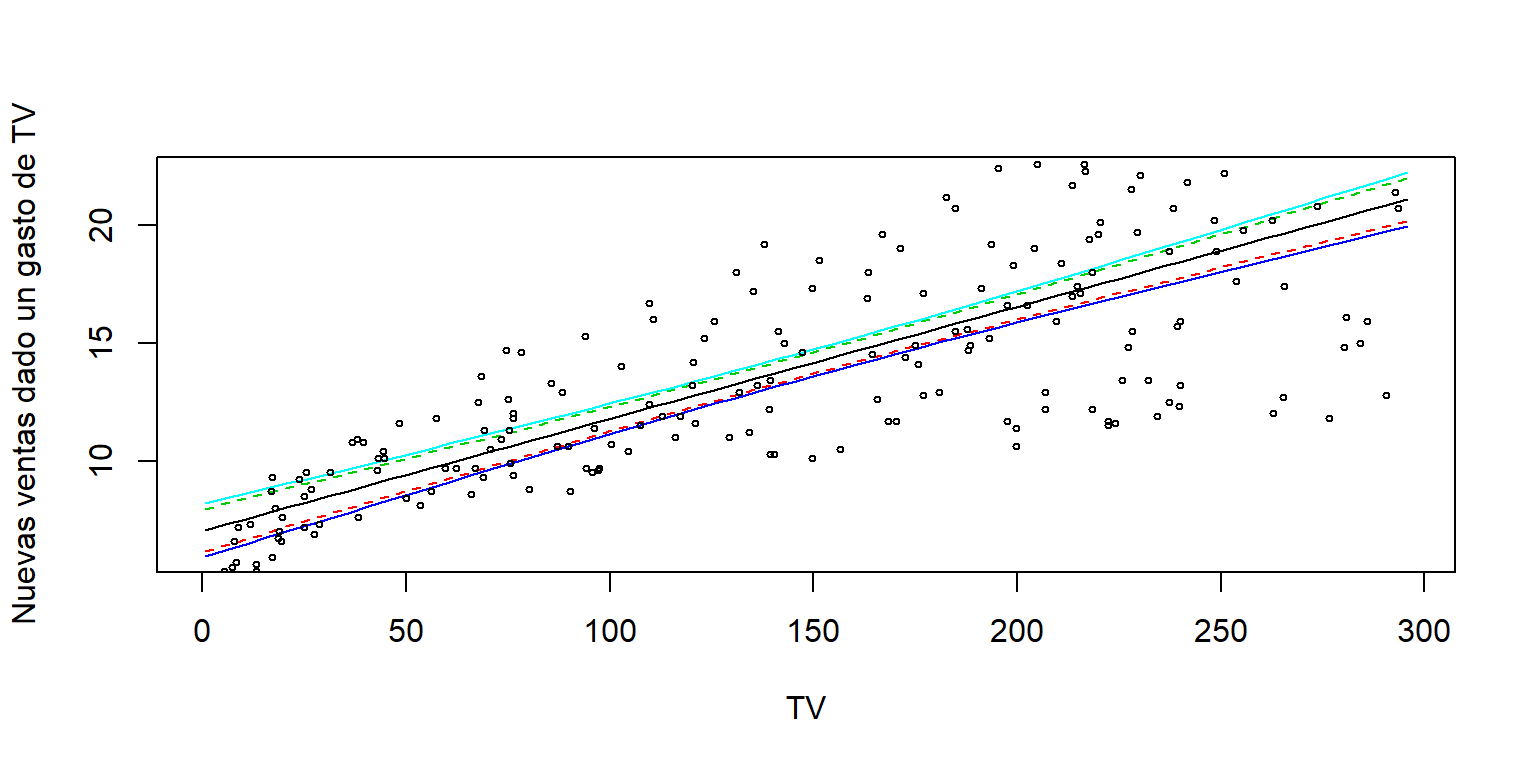
Nota: no se pueden obtener bandas de predicción sobre \(x\), pues el método de Scheffé y de Bonferroni dependen de \(k\), a diferencia de bandas de confianza donde el método de Scheffé no depende de \(k\).
Nota 2. Se pueden obtener intervalos de confianza de \(k\) combinaciones lineales usando el paquete multcomp por el método del máximo módulo; los de Bonferroni y Scheffé se pueden calcular dando el valor del cuantil asociado.
library(multcomp)
newdata <- data.frame(TV = c(xh1, xh2, xh3))
#Para alpha
K=matrix(c(1,1,1,xh1, xh2, xh3), ncol=2, nrow=3)
m2=0
prueba1=glht(fit1, linfct=K, rhs=m2)
#Máximo modulo
confint(prueba1)##
## Simultaneous Confidence Intervals
##
## Fit: lm(formula = sales ~ TV, data = Datos)
##
## Quantile = 2.3618755
## 95% family-wise confidence level
##
##
## Linear Hypotheses:
## Estimate lwr upr
## 1 == 0 7.0658692 5.9883428 8.1433956
## 2 == 0 14.0225000 13.4782724 14.5667276
## 3 == 0 21.1224538 20.0283481 22.2165595#Bonferroni
confint(prueba1, calpha=qt(1-.05/(2*length(newdata$TV)), n-2,lower.tail = TRUE) )##
## Simultaneous Confidence Intervals
##
## Fit: lm(formula = sales ~ TV, data = Datos)
##
## Quantile = 2.4144918
## 95% confidence level
##
##
## Linear Hypotheses:
## Estimate lwr upr
## 1 == 0 7.0658692 5.9643384 8.1674000
## 2 == 0 14.0225000 13.4661485 14.5788515
## 3 == 0 21.1224538 20.0039743 22.2409332#Scheffé
confint(prueba1, calpha=sqrt(2*qf(1-delta,2 ,n-2,lower.tail = TRUE) ) )##
## Simultaneous Confidence Intervals
##
## Fit: lm(formula = sales ~ TV, data = Datos)
##
## Quantile = 2.4663813
## 95% confidence level
##
##
## Linear Hypotheses:
## Estimate lwr upr
## 1 == 0 7.0658692 5.9406656 8.1910728
## 2 == 0 14.0225000 13.4541920 14.5908080
## 3 == 0 21.1224538 19.9799373 22.2649703library(investr)
pred.w.climBon=predFit(fit1, newdata, interval = "confidence", level = 0.95, adjust = c("Bonferroni"),k=length(newdata$TV) )
head(pred.w.climBon)## fit lwr upr
## 1 7.065869197 5.964338438 8.167399957
## 2 14.022500000 13.466148460 14.578851540
## 3 21.122453773 20.003974340 22.240933207pred.w.climScheffe=predFit(fit1, newdata, interval = "confidence", level = 0.95, adjust = c("Scheffe") )
head(pred.w.climScheffe)## fit lwr upr
## 1 7.065869197 5.940665596 8.191072799
## 2 14.022500000 13.454191988 14.590808012
## 3 21.122453773 19.979937257 22.264970290