Regresión lineal simple (3/4)
Gonzalo Pérez
3 de marzo de 2020
Calibración a partir del modelo de regresión lineal simple
Ejemplo.
Determinar las cantidades de substancias tóxicas en muestras de agua es en algunas ocasiones un problema difícil. Supongamos que un investigador tiene 32 muestras de agua en su laboratorio, de cada una tiene el valor “real” de cantidad de arsénico (quizás incluyó esa cantidad en su experimento o las midió con mucha precisión), además tiene una medición de la cantidad de arsénico tomada mediante un procedimiento sujeto a cierto error que se usará en campo.
library(investr)
Datos=arsenic
head(Datos)## actual measured
## 1 0 0.17
## 2 0 0.25
## 3 0 0.01
## 4 0 0.12
## 5 1 1.25
## 6 1 0.86str(Datos)## 'data.frame': 32 obs. of 2 variables:
## $ actual : int 0 0 0 0 1 1 1 1 2 2 ...
## $ measured: num 0.17 0.25 0.01 0.12 1.25 0.86 1.25 1.1 2.01 2.03 ...De acuerdo con las 32 observaciones considera que un modelo de regresión lineal simple es adecuado, en donde la medición del total de arsénico realizada con el procedimiento de campo (y=measured) tiene cierto error, para cada valor “real” de la cantidad de arsénico (x=actual).
Suponga ahora, que el investigador tiene una nueva muestra de agua donde se ha medido la cantidad de arsénico con el procedimiento de campo, \(y_h= 3.0\). El investigador está interesado en inferir la cantidad “real” de arsénico presente en la muestra de agua.
Notar que en este contexto, la cantidad “real” de arsénico en la muestra no necesariamente se puede considerar como una variable aleatoria que depende de la cantidad de arsénico medido con el procedimiento de campo.
fit1=lm(measured~actual, data=Datos)
summary(fit1)##
## Call:
## lm(formula = measured ~ actual, data = Datos)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.4454 -0.0860 0.0116 0.1407 0.3023
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.1046 0.0605 1.73 0.094 .
## actual 0.9877 0.0145 68.29 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.19 on 30 degrees of freedom
## Multiple R-squared: 0.994, Adjusted R-squared: 0.993
## F-statistic: 4.66e+03 on 1 and 30 DF, p-value: <2e-16El paquete investr nos permite obtener un intervalo para \(x_h\) usando dos métodos
- Método de inversión (cuando sólo se tiene una observación coincide con la inversión del Intervalo de predicción)
- Método delta
(yh=c(3))## [1] 3Esto se realiza a partir de la función calibrate
options(digits=3)
(res=calibrate(fit1, y0=yh, interval="inversion", level=.95 ) )## estimate lower upper
## 2.93 2.54 3.33Se puede verificar que este intervalo corresponde a la inversión del intervalo de predicción:
plotFit(fit1, interval="prediction", level=.95, shade=TRUE, col.pred="skyblue")
abline(h=3, v=c(res$lower, res$estimate, res$upper), lty=2 )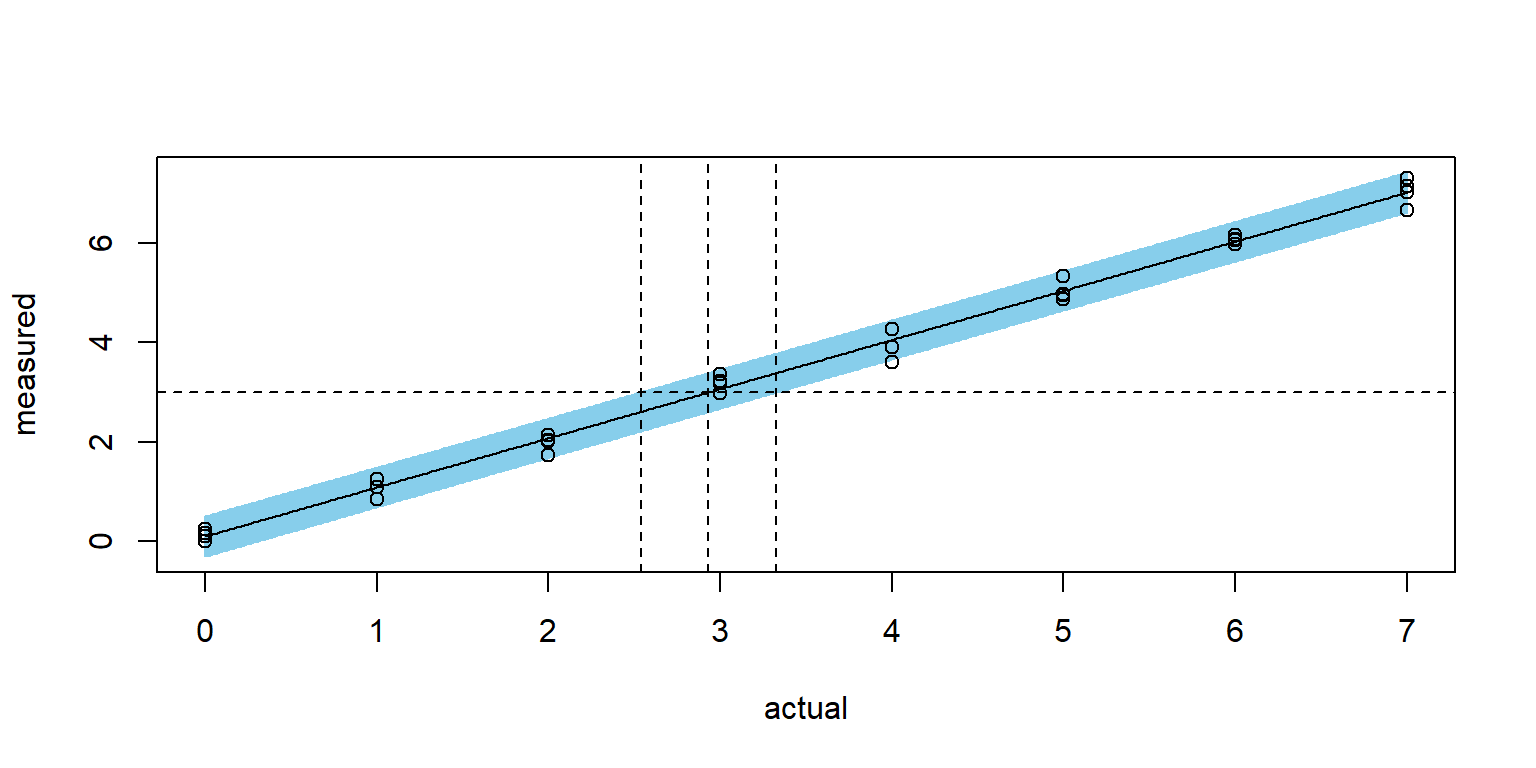
Usando el método de Delta (o intervalo tipo Wald)
(res=calibrate(fit1, y0=yh, interval="Wald", level=.95 ) )## estimate lower upper se
## 2.931 2.537 3.325 0.193Nota. Este método se basa en supuestos asintóticos y siempre existe a diferencia del método de inversión.
Si por ejemplo, a la nueva muestra de agua se le hubieran realizado tres mediciones independientes resultando en \(y_{h1}= 3.17, y_{h2}= 3.09, y_{h3}= 3.16\) (notar que la independencia de los errores está en las mediciones realizadas por el procedimiento).
(yh=c(3.17, 3.09, 3.16))## [1] 3.17 3.09 3.16(res=calibrate(fit1, y0=yh, interval="inversion", level=.95 ) )## estimate lower upper
## 3.07 2.85 3.30Y si esas mediciones se realizarán sobre diferentes muestras de agua, entonces quizás se tendría interés en identificar de forma simultánea los valores actuales de arsénico para las tres muestras (supongamos que pertenecen a tres partes de un río, quizás se quiere saber si alguna de las tres rebasan cierto nivel de arsénico, pues entonces esa parte del río estaría contaminado).
(yh=c(3.17, 3.09, 3.16))## [1] 3.17 3.09 3.16delta=.05/3
(res=calibrate(fit1, y0=yh[1], interval="inversion", level=1-delta ) )## estimate lower upper
## 3.10 2.61 3.59(res=calibrate(fit1, y0=yh[2], interval="inversion", level=1-delta ) )## estimate lower upper
## 3.02 2.53 3.51(res=calibrate(fit1, y0=yh[3], interval="inversion", level=1-delta ) )## estimate lower upper
## 3.09 2.60 3.58El paquete también permite calcular el valor de \(x_h\) para un valor esperado de \(y\), es decir, a partir de plantear el problema de querer saber cual sería el valor de \(x_h\) que en promedio produce el valor \(y_h\).
En este caso se debe agregar en calibrate el argumento: mean.response =TRUE
Ejercicio.
Se realizó un experimento en el cual el peso en gramos de 14 cristales fue medido después de dejar crecer el cristal por cierto (predeterminado) tiempo en horas. Se asume que dado un tiempo particular que se deja crecer el cristal el peso del cristal observado es aleatorio.
Suponga que una empresa se ha comprometido en vender ese cristal, de manera que cada unidad en promedio pesa 8 gramos ¿cuál sería el tiempo en horas que permitiría obtener cristales que en promedio pesen 8 gramos?
Datos=crystal
head(Datos)## time weight
## 1 2 0.08
## 2 4 1.12
## 3 6 4.43
## 4 8 4.98
## 5 10 4.92
## 6 12 7.18str(Datos)## 'data.frame': 14 obs. of 2 variables:
## $ time : num 2 4 6 8 10 12 14 16 18 20 ...
## $ weight: num 0.08 1.12 4.43 4.98 4.92 ...