Regresión lineal simple (4/4)

Análisis de residuales y verificación de supuestos del modelo.

En el modelo de regresión lineal simple se hacen principalmente los siguientes supuestos:

• Relación lineal entre la variable \(X\) y \(Y\).
• Errores independientes
• Errores con la misma varianza (homocedasticidad)
• Distribución normal de los errores

Otros problemas potenciales que se pueden encontrar son outliers (generalmente en la variable \(Y\)) y valores influyentes (en la variable \(X\)).

La mayoría de estos supuestos se realiza de forma gráfica y usando los residuales (o errores estimados) o adaptaciones de éstos.

Relación lineal entre la variable \(X\) y \(Y\).

Esta revisión se puede realizar en la regresión lineal simple directamente observando el scatterplot de los datos \(X\) y \(Y\).

library(ISLR)
Datos=read.csv("images/archivos/Advertising.csv", header=TRUE, sep="," )
require(ggplot2)
require(ggiraph)
require(ggiraphExtra)
ggPoints(aes(x=TV,y=sales),method="lm", data=Datos,interactive=TRUE)

Sin embargo, es muy común usar también la gráfica de los residuales \(y_i-\hat{y}_i\) contra los valores ajustados \(\hat{y}_i\). El objeto obtenido al usar la función lm en R tiene preestablecidas varias gráficas que sirven para los análisis.

fit1=lm(sales~TV, data=Datos)
summary(fit1)

## 
## Call:
## lm(formula = sales ~ TV, data = Datos)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -8.386 -1.955 -0.191  2.067  7.212 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  7.03259    0.45784    15.4   <2e-16 ***
## TV           0.04754    0.00269    17.7   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 3.3 on 198 degrees of freedom
## Multiple R-squared:  0.612,  Adjusted R-squared:  0.61 
## F-statistic:  312 on 1 and 198 DF,  p-value: <2e-16

plot(fit1, 1)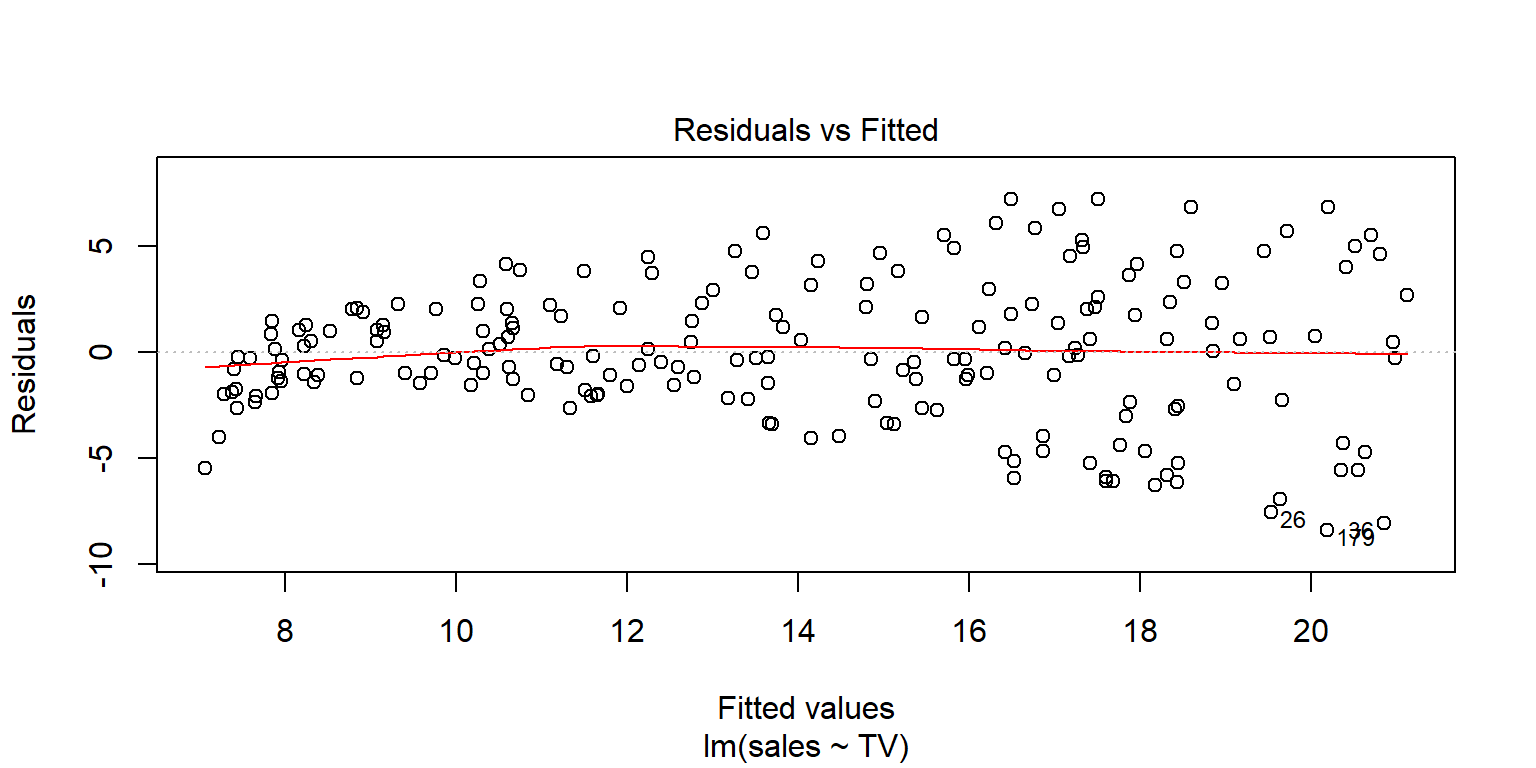

En este caso, lo ideal sería que los residuales no muestren ningún patrón con respecto a no seguir en promedio una línea horizontal con media cero. En el ejemplo, se puede observar que para los valores pequeños parece que hay una distorsión, aunque en general no es mucha, el patrón más marcado está sobre un crecimiento en la variabilidad de los residuales.

Opciones para arreglar la linealidad son considerar transformaciones a los datos, ya sea a la variable \(X\), a la variable \(Y\) o ambas.

Datos$Xprima=sqrt(Datos$TV)

fit2=lm(sales~Xprima, data=Datos)
summary(fit2)

## 
## Call:
## lm(formula = sales ~ Xprima, data = Datos)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -7.430 -1.953 -0.109  1.939  7.764 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    2.672      0.667     4.0  8.8e-05 ***
## Xprima         0.995      0.055    18.1  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 3.2 on 198 degrees of freedom
## Multiple R-squared:  0.623,  Adjusted R-squared:  0.621 
## F-statistic:  327 on 1 and 198 DF,  p-value: <2e-16

plot(fit2, 1)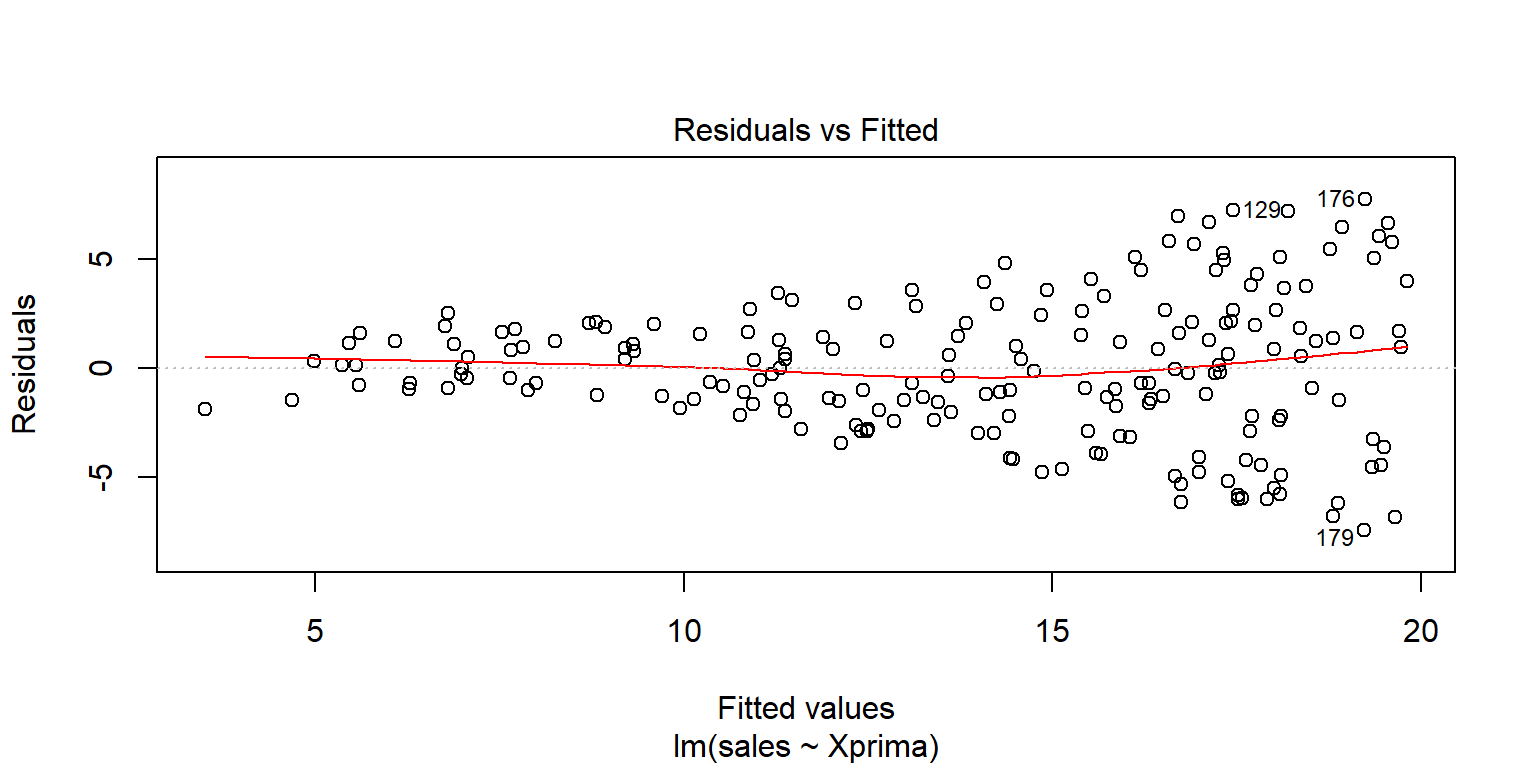

ggPoints(aes(x=Xprima,y=sales),method="lm", data=Datos,interactive=TRUE)

Lo anterior parece arreglar la linealidad, pero no la variabilidad no constante en \(Y\).

Una tranformación polinomial también podría ser una opción, aunque eso ya es regresión lineal múltiple

Datos$Xprima2=Datos$TV^2
Datos$Xprima3=Datos$TV^3

fit3=lm(sales~TV+Xprima2+Xprima3, data=Datos)
summary(fit3)

## 
## Call:
## lm(formula = sales ~ TV + Xprima2 + Xprima3, data = Datos)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
##  -7.97  -1.89  -0.09   2.02   7.38 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  5.42e+00   8.64e-01    6.27  2.2e-09 ***
## TV           9.64e-02   2.58e-02    3.74  0.00024 ***
## Xprima2     -3.15e-04   2.02e-04   -1.56  0.12056    
## Xprima3      5.57e-07   4.49e-07    1.24  0.21652    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 3.2 on 196 degrees of freedom
## Multiple R-squared:  0.622,  Adjusted R-squared:  0.616 
## F-statistic:  108 on 3 and 196 DF,  p-value: <2e-16

plot(fit3, 1)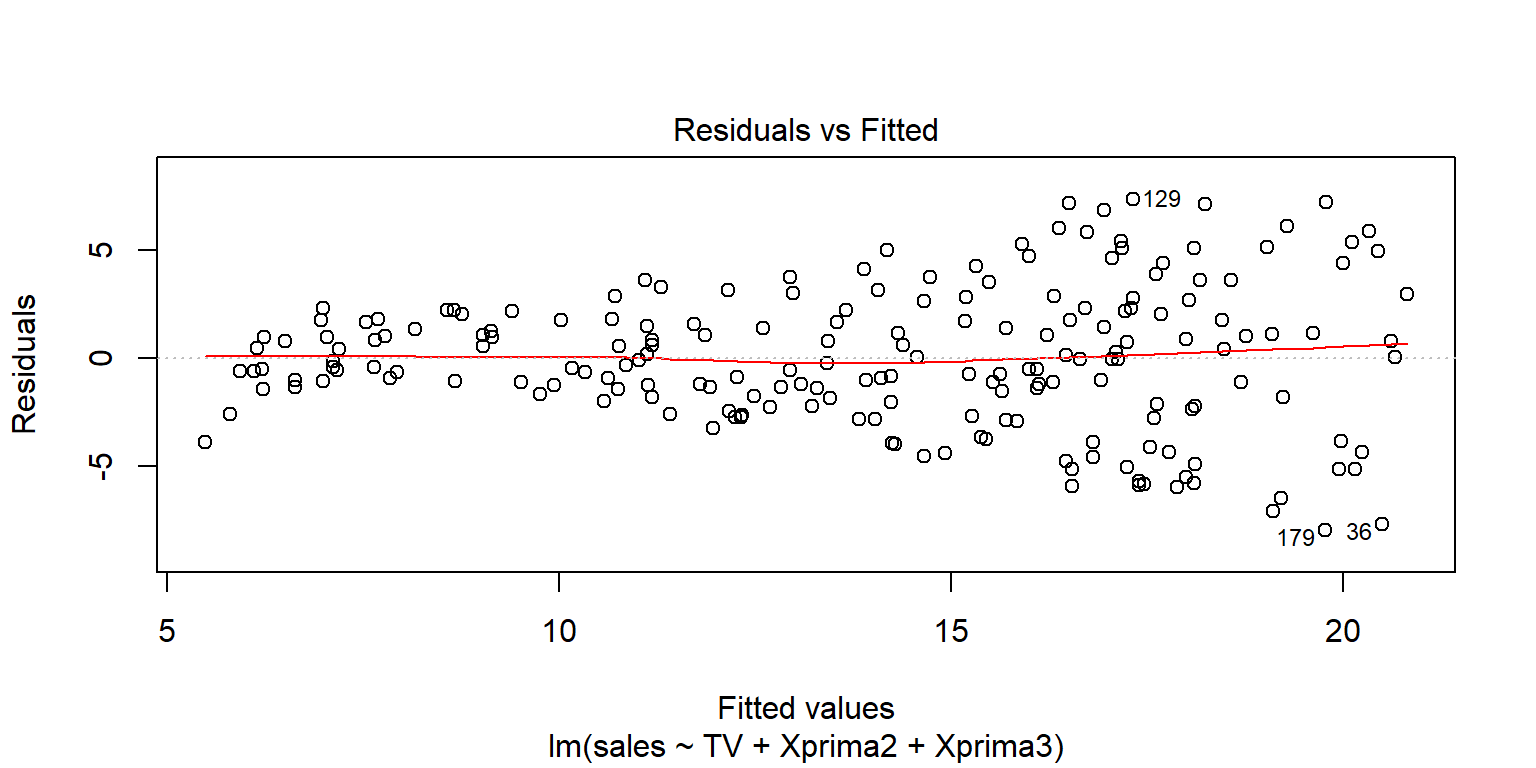

ggplot(data=Datos, aes(x=TV,y=sales))+
   geom_smooth(method="lm", se=FALSE, colour="red", formula=y~x)+
  geom_smooth(method="lm", se=FALSE, colour="blue", formula=y~x+I(x^2)+I(x^3))+
  geom_point(colour="black")

A veces es conveniente transformar la variable \(Y\), con suerte eso eliminaría la varianza no constante.

library(car)

fit1Ymod=boxCox(fit1, plotit=TRUE)

Datos$Yprima=( (Datos$sales)^(.5)-1 )/.5
Datos$Yprima2=bcPower(Datos$sales, .5)

fit4=lm(Yprima~TV, data=Datos)
summary(fit4)

## 
## Call:
## lm(formula = Yprima ~ TV, data = Datos)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -2.8991 -0.5049  0.0234  0.6365  1.7001 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 3.419720   0.121136    28.2   <2e-16 ***
## TV          0.013156   0.000712    18.5   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.86 on 198 degrees of freedom
## Multiple R-squared:  0.633,  Adjusted R-squared:  0.631 
## F-statistic:  342 on 1 and 198 DF,  p-value: <2e-16

plot(fit4, 1)

datonuevos= data.frame(TV=seq(0, 300, by=.2), Yprima=predict(fit4, newdata=data.frame(TV=seq(0, 300, by=.2) ) ))

datonuevos$sales=(.5*(datonuevos$Yprima)+1)^2
ggPoints(aes(x=TV,y=Yprima),method="lm", data=Datos,interactive=TRUE)

ggplot(data=Datos, aes(x=TV,y=sales))+
   geom_smooth(method="lm", se=FALSE, colour="red", formula=y~x)+
  geom_smooth(method="lm", se=FALSE, colour="blue", formula=y~I(x^(.5)))+
  geom_point(colour="black")+
  geom_line(data= datonuevos, colour="green" )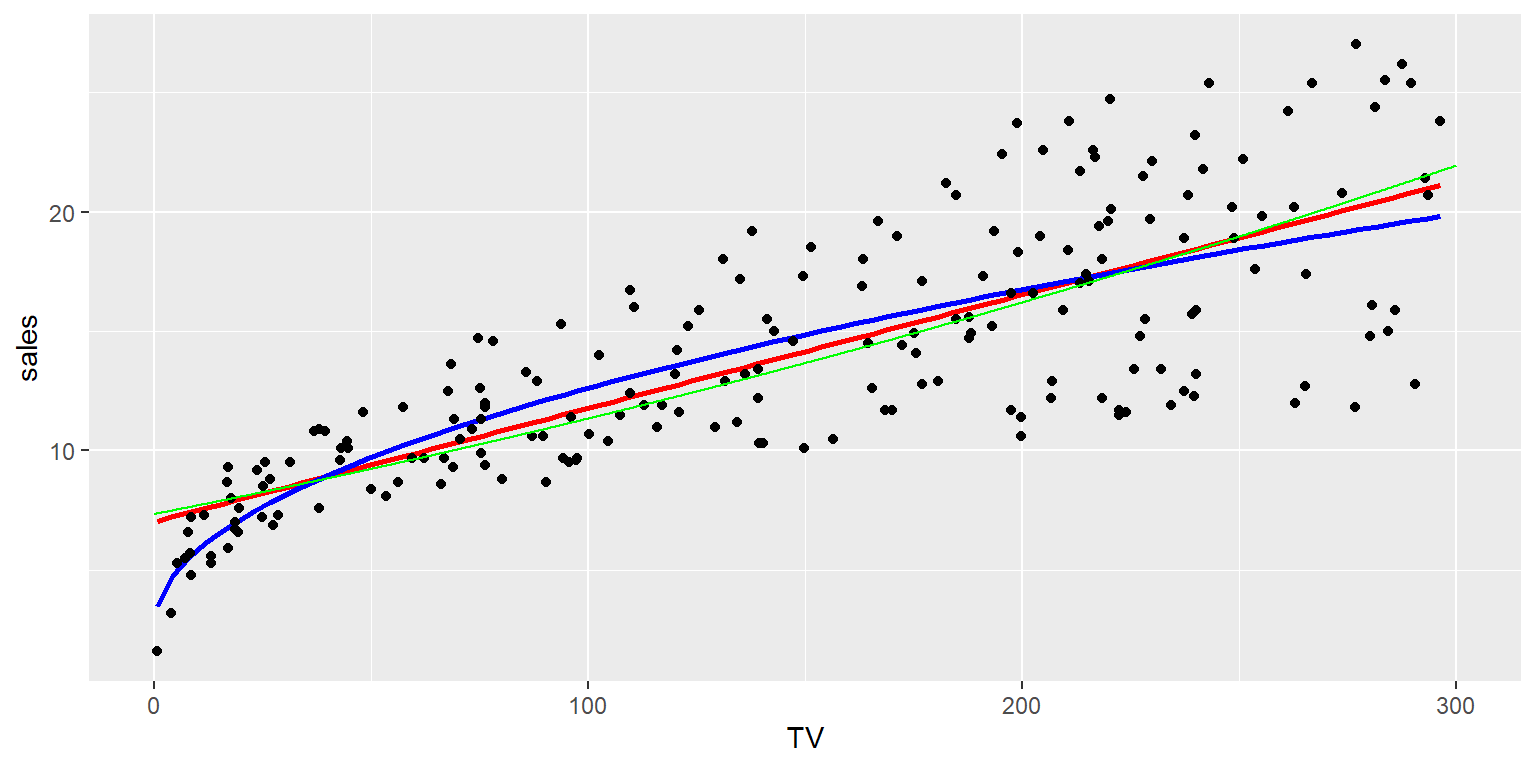

boxTidwell(Yprima~TV, data=Datos)

##  MLE of lambda Score Statistic (z) Pr(>|z|)    
##            0.3                  -4    6e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## iterations =  4

Datos$Xprimab=Datos$TV^(.3)

fit5=lm(Yprima~Xprimab, data=Datos)
summary(fit5)

## 
## Call:
## lm(formula = Yprima ~ Xprimab, data = Datos)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -1.8267 -0.5371  0.0111  0.5710  1.6940 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   0.5526     0.2416    2.29    0.023 *  
## Xprimab       1.1373     0.0556   20.46   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.81 on 198 degrees of freedom
## Multiple R-squared:  0.679,  Adjusted R-squared:  0.677 
## F-statistic:  418 on 1 and 198 DF,  p-value: <2e-16

plot(fit5, 1)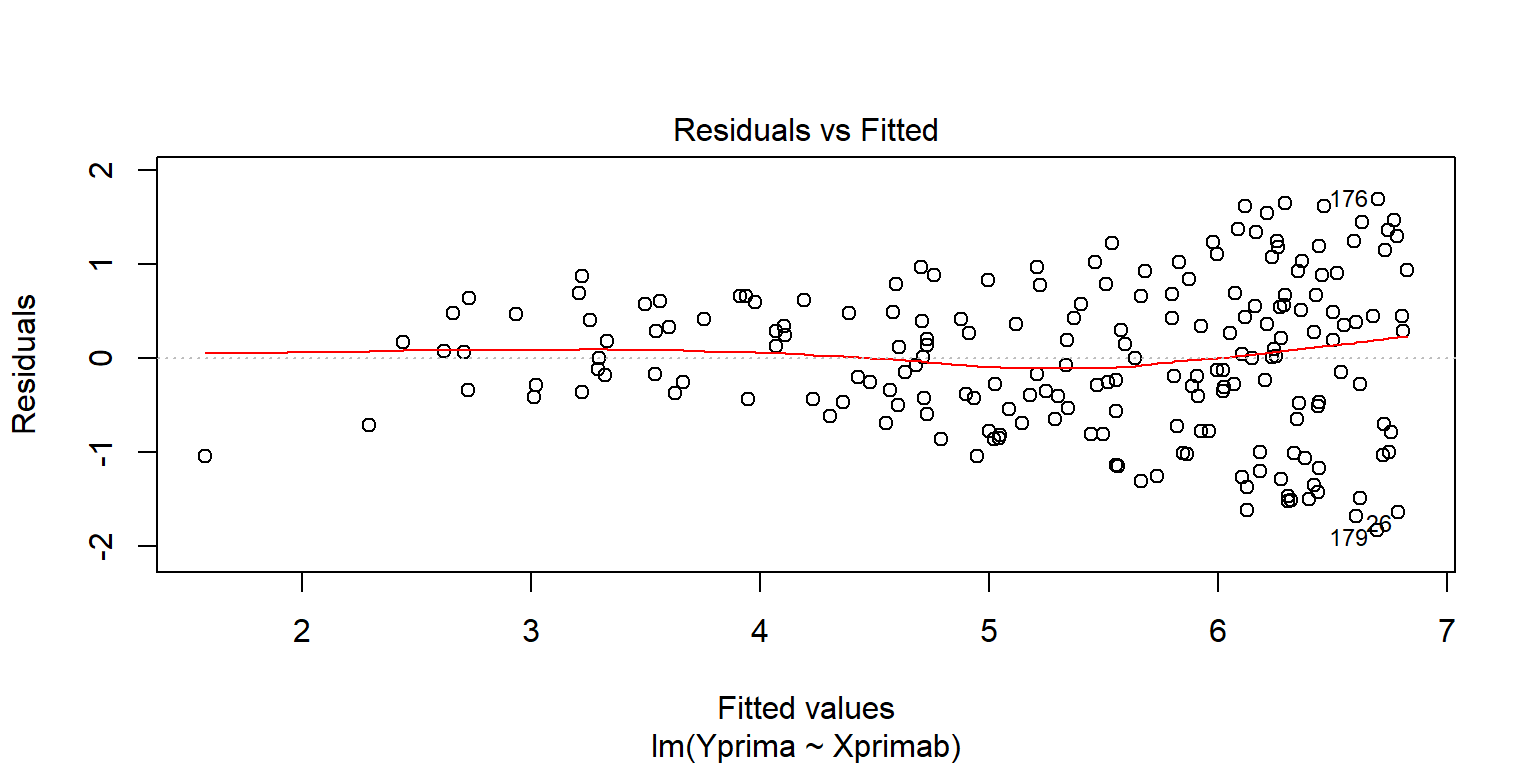

datonuevos= data.frame(Xprimab=seq(0, 5.5, by=.2), Yprima=predict(fit5, newdata=data.frame(Xprimab=seq(0, 5.5, by=.2) ) ))
datonuevos$TV=(datonuevos$Xprimab)^(1/.3)
datonuevos$sales=(.5*(datonuevos$Yprima)+1)^2
ggPoints(aes(x=Xprimab,y=Yprima),method="lm", data=Datos,interactive=TRUE)

ggplot(data=Datos, aes(x=TV,y=sales))+
   geom_smooth(method="lm", se=FALSE, colour="red", formula=y~x)+
  geom_smooth(method="lm", se=FALSE, colour="blue", formula=y~I(x^(.5)))+
  geom_point(colour="black")+
  geom_line(data= datonuevos, colour="green" )

Homocedasticidad

Se usa la gráfica de los residuales estandarizados contra los valores ajustados \(\hat{y}_i\). Se busca que los errores se distribuyan sin ningún patrón

plot(fit1, 3)

plot(fit2, 3)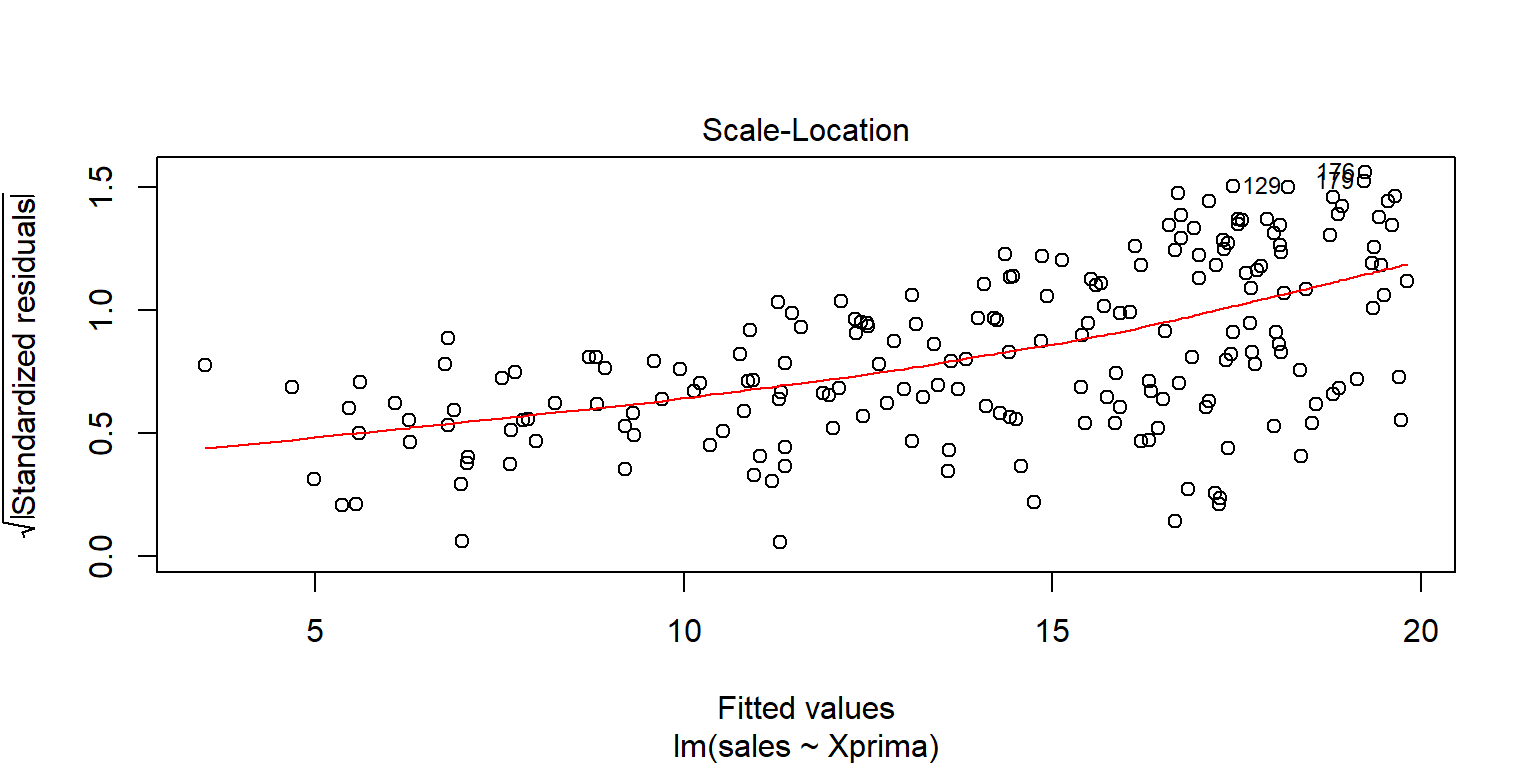

Existen algunas pruebas que pueden ayudar.

• Breush Pagan Test. \(H_0\): La varianza de los residuales no depende de las variables en el modelo, es decir, es constante.

library(lmtest)
lmtest::bptest(fit1)

## 
##  studentized Breusch-Pagan test
## 
## data:  fit1
## BP = 48, df = 1, p-value = 4e-12

lmtest::bptest(fit2)

## 
##  studentized Breusch-Pagan test
## 
## data:  fit2
## BP = 53, df = 1, p-value = 3e-13

• Score Test

library(car)
car::ncvTest(fit1)

## Non-constant Variance Score Test 
## Variance formula: ~ fitted.values 
## Chisquare = 43, Df = 1, p = 6e-11

car::ncvTest(fit2)

## Non-constant Variance Score Test 
## Variance formula: ~ fitted.values 
## Chisquare = 46, Df = 1, p = 1e-11

Errores independientes

library(broom)
Datosfit1=augment(fit1)
head(Datosfit1)

## # A tibble: 6 x 9
##   sales    TV .fitted .se.fit .resid    .hat .sigma   .cooksd .std.resid
##   <dbl> <dbl>   <dbl>   <dbl>  <dbl>   <dbl>  <dbl>     <dbl>      <dbl>
## 1  22.1 230.    18.0    0.321  4.13  0.00970   3.25 0.00794       1.27  
## 2  10.4  44.5    9.15   0.359  1.25  0.0122    3.27 0.000920      0.387 
## 3   9.3  17.2    7.85   0.419  1.45  0.0165    3.27 0.00169       0.449 
## 4  18.5 152.    14.2    0.231  4.27  0.00501   3.25 0.00434       1.31  
## 5  12.9 181.    15.6    0.248 -2.73  0.00578   3.26 0.00205      -0.839 
## 6   7.2   8.7    7.45   0.438 -0.246 0.0180    3.27 0.0000534    -0.0762

acf(Datosfit1$.std.resid)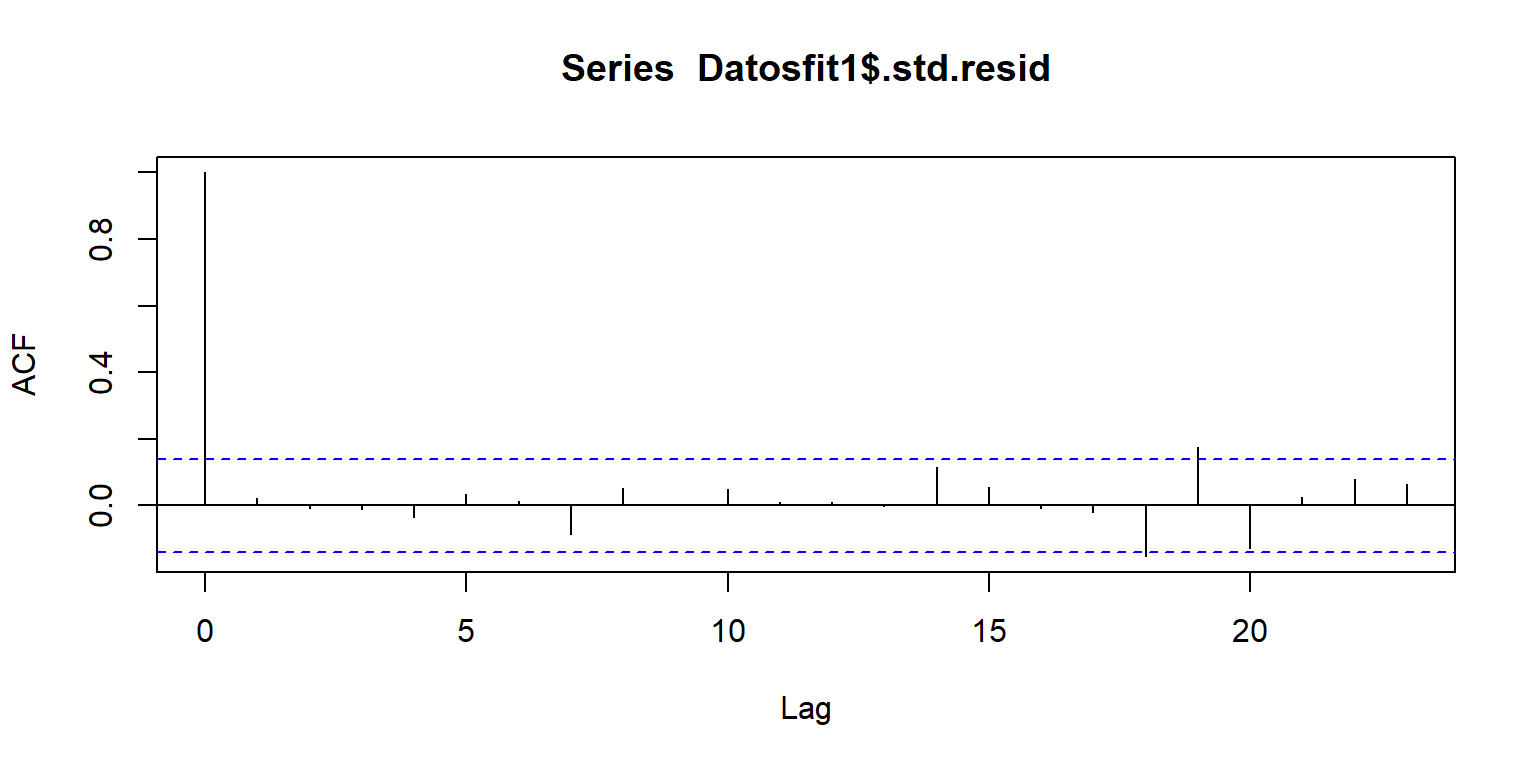

Algunas pruebas

Prueba de rachas. \(H_0\) los datos son aleatorios

library(lawstat)
lawstat::runs.test(Datosfit1$.std.resid)

## 
##  Runs Test - Two sided
## 
## data:  Datosfit1$.std.resid
## Standardized Runs Statistic = -1, p-value = 0.3

library(randtests)
randtests::runs.test(Datosfit1$.std.resid)

## 
##  Runs Test
## 
## data:  Datosfit1$.std.resid
## statistic = -1, runs = 94, n1 = 100, n2 = 100, n = 200, p-value = 0.3
## alternative hypothesis: nonrandomness

Prueba Durbin-Watson. \(H_0\) los errores no están autocorrelacionados.

lmtest::dwtest(fit1)

## 
##  Durbin-Watson test
## 
## data:  fit1
## DW = 2, p-value = 0.3
## alternative hypothesis: true autocorrelation is greater than 0

Normalidad de los residuales

Por lo general se revisa con una qq-plot de los errores estandarizados. lm tiene una gráfica directa. Se desea que los puntos estén sobre la línea recta dibujada.

plot(fit1, 2)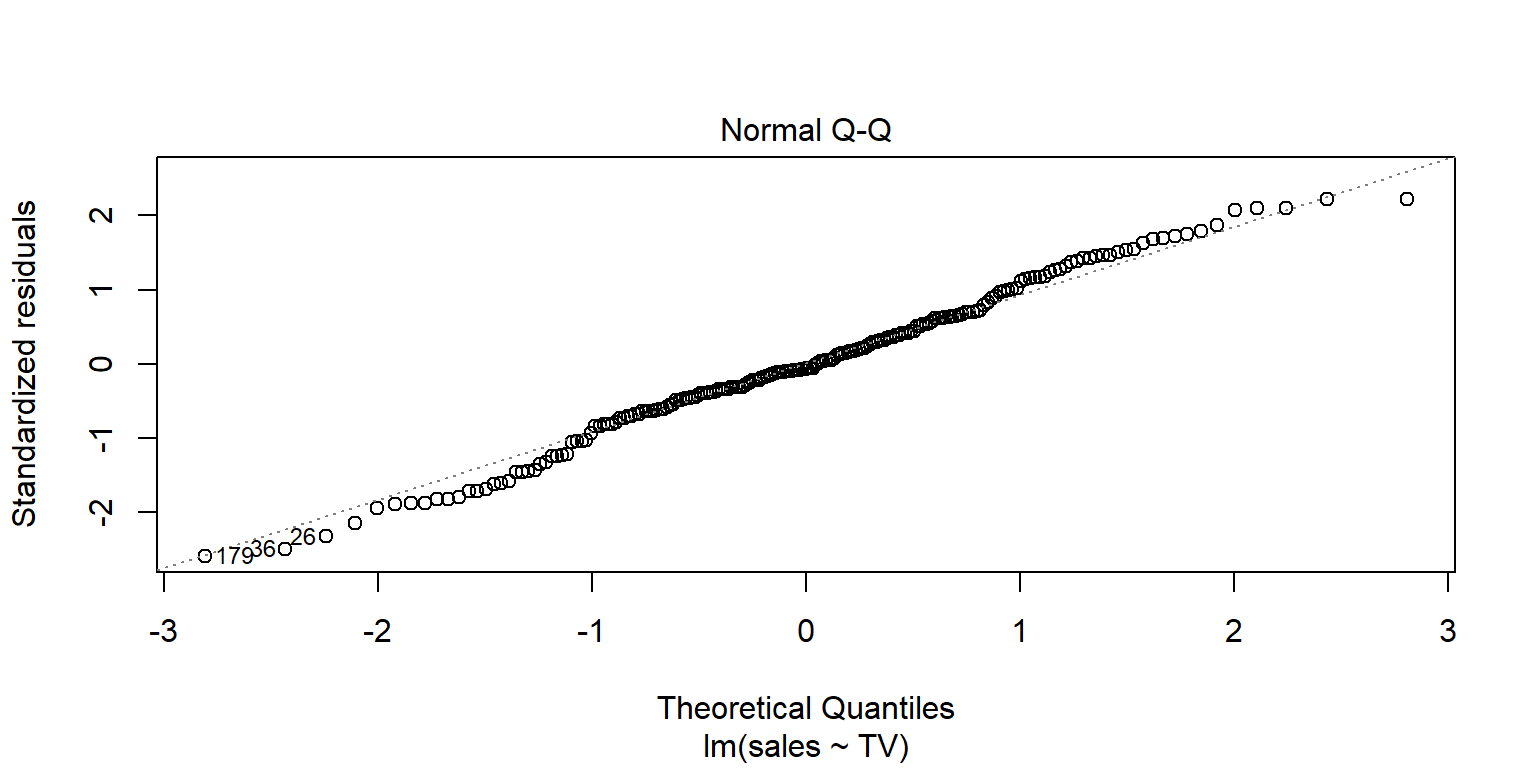

Algunos test. \(H_0\): los valores son normales.

shapiro.test(Datosfit1$.std.resid)

## 
##  Shapiro-Wilk normality test
## 
## data:  Datosfit1$.std.resid
## W = 1, p-value = 0.2

library(nortest)

nortest::lillie.test(Datosfit1$.std.resid)

## 
##  Lilliefors (Kolmogorov-Smirnov) normality test
## 
## data:  Datosfit1$.std.resid
## D = 0.04, p-value = 0.5

library(normtest)
normtest::jb.norm.test(Datosfit1$.std.resid)

## 
##  Jarque-Bera test for normality
## 
## data:  Datosfit1$.std.resid
## JB = 0.7, p-value = 0.7

Outliers y valores influyentes

• Outliers se pueden observar con la gráfica de residuales estandarizados. En general, se consideran que los residuales más grandes de 2 (3) podrían ser outliers.

• Existen algunas observaciones cuyo valor es extremo en la variable predictora. Se recomienda revisar la estadística leverage. En general, si esta estadística es superior a \(4/n\) se dice que tiene un valor muy grande en \(X\).

• Las observaciones influyentes son aquellas que al eliminarlas pueden alterar los resultados de la regresión. Una metrica para analizar estos valores se conoce como Cook’s distance. Una regla empírica es considerar como observación influyente si esta distancia excede \(4/(n-2)\).

En R, existe una gráfica que resume lo anterior

plot(fit1, 5)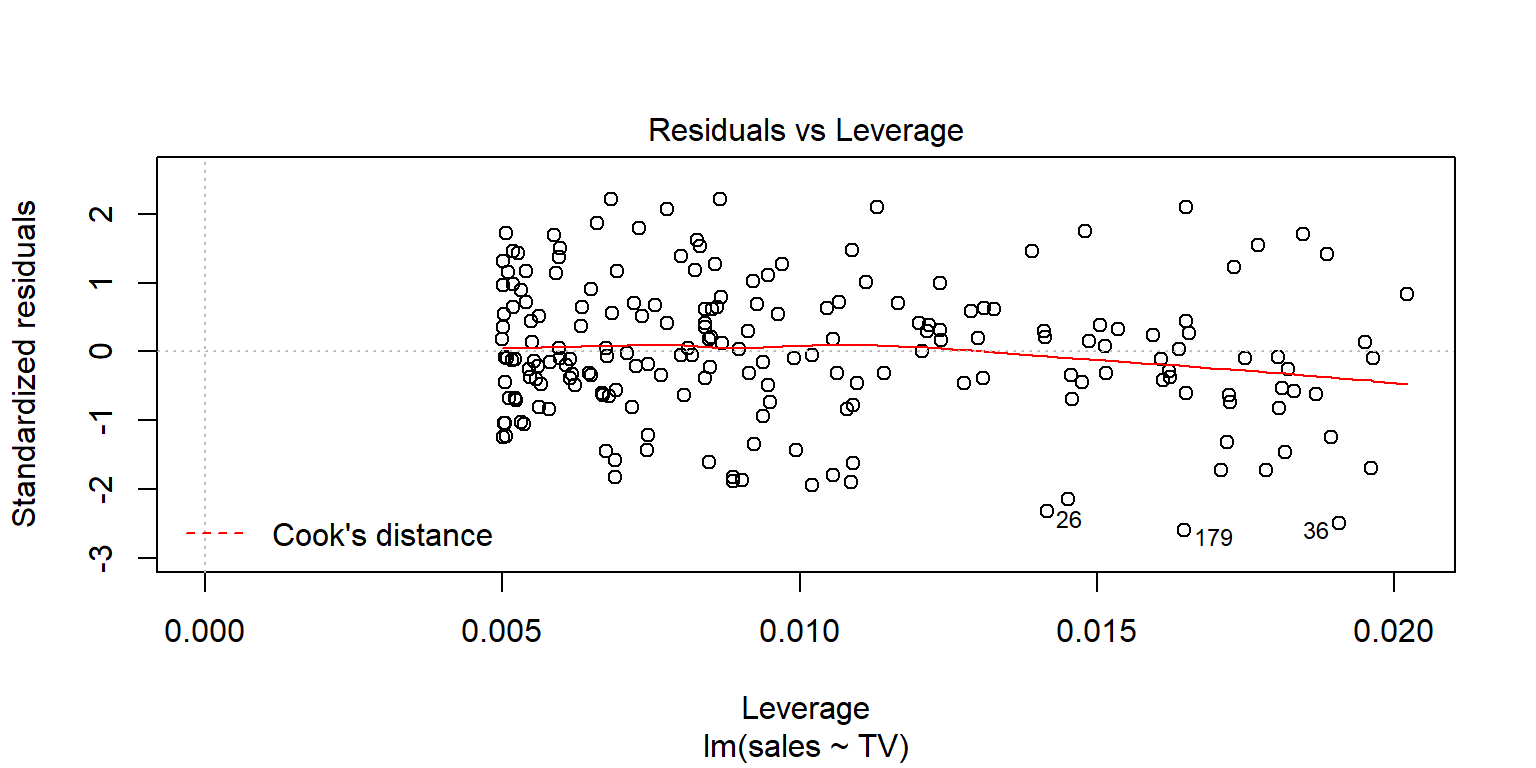

plot(fit1, 4)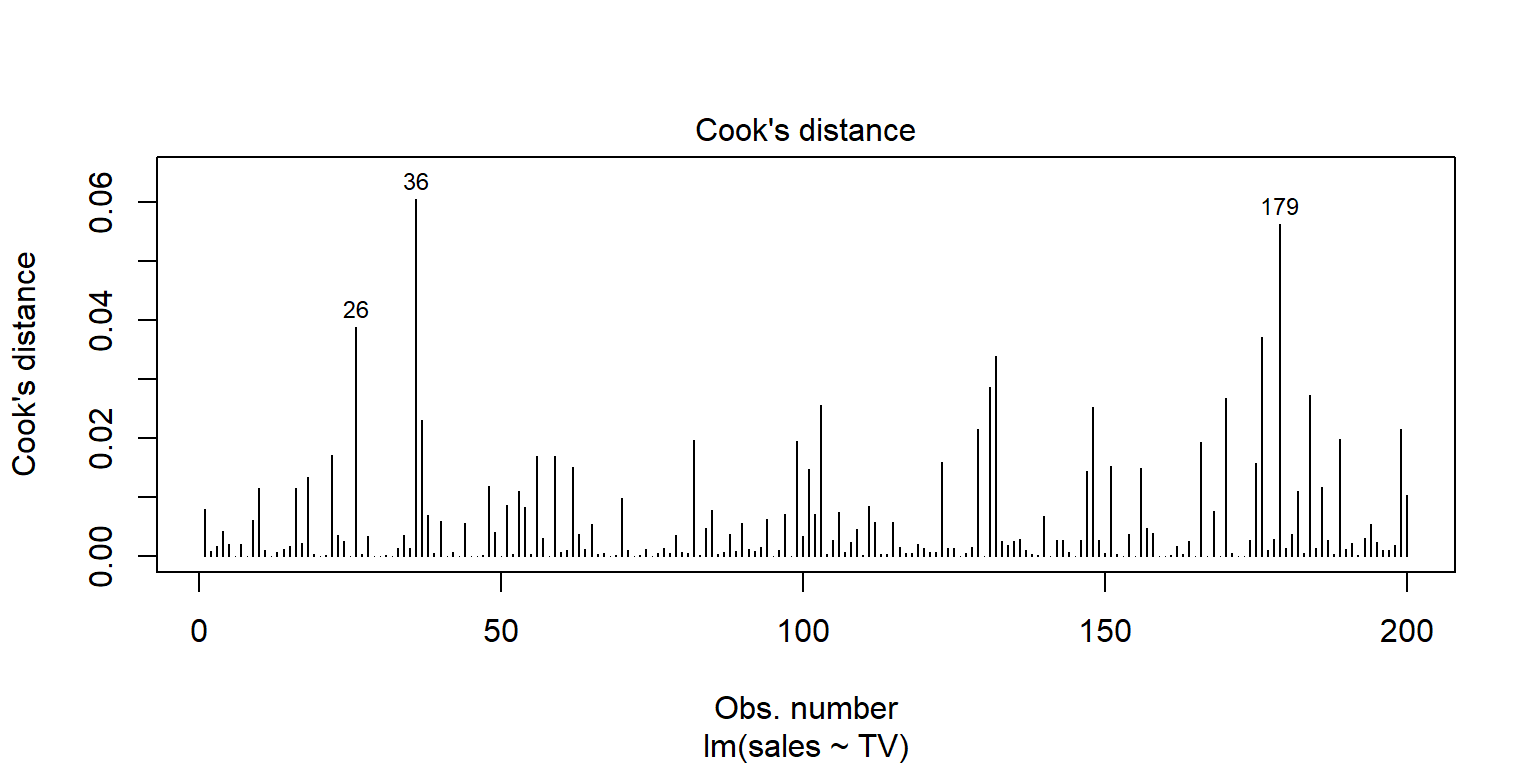

Otro paquete

library(olsrr)
ols_plot_diagnostics(fit1)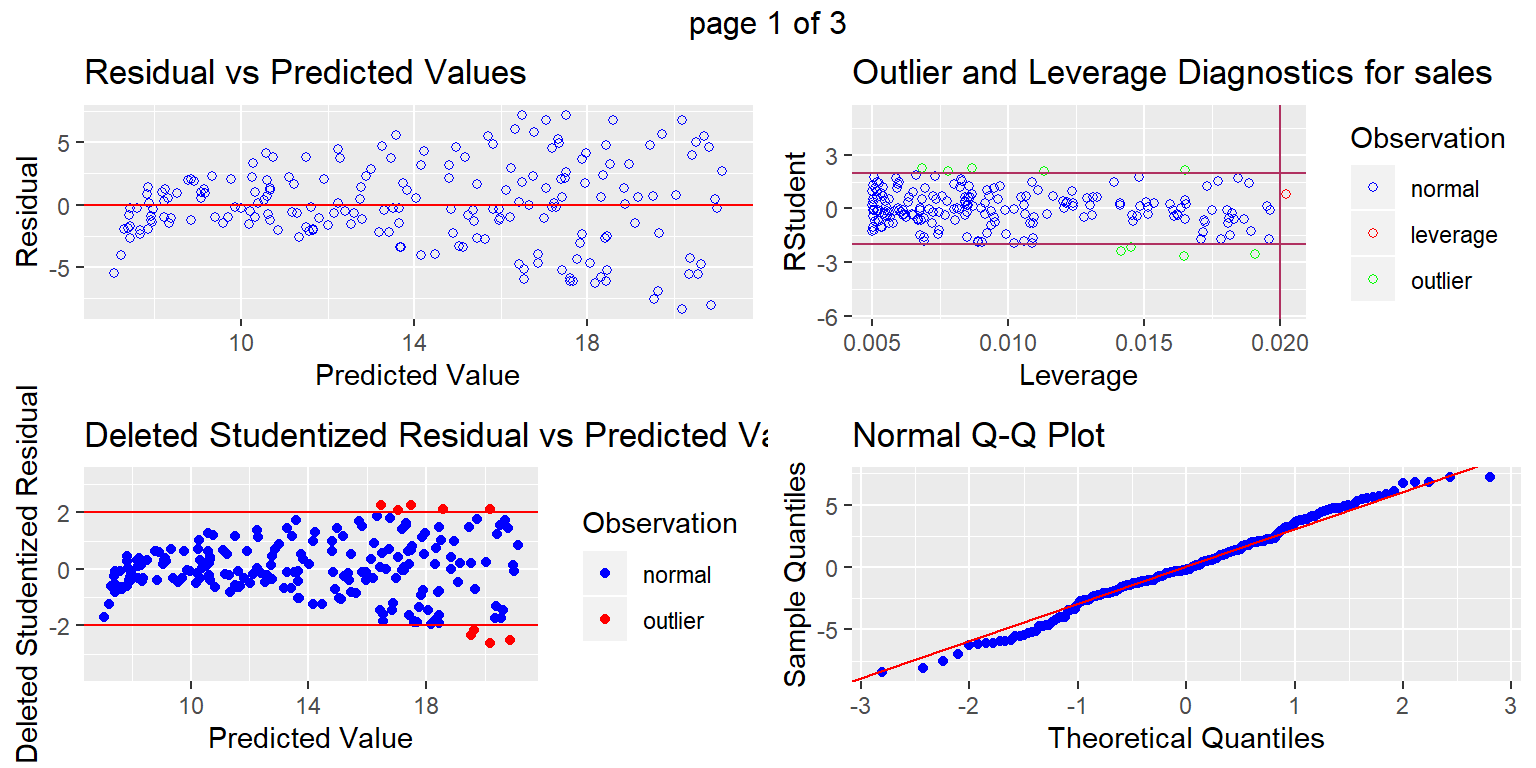

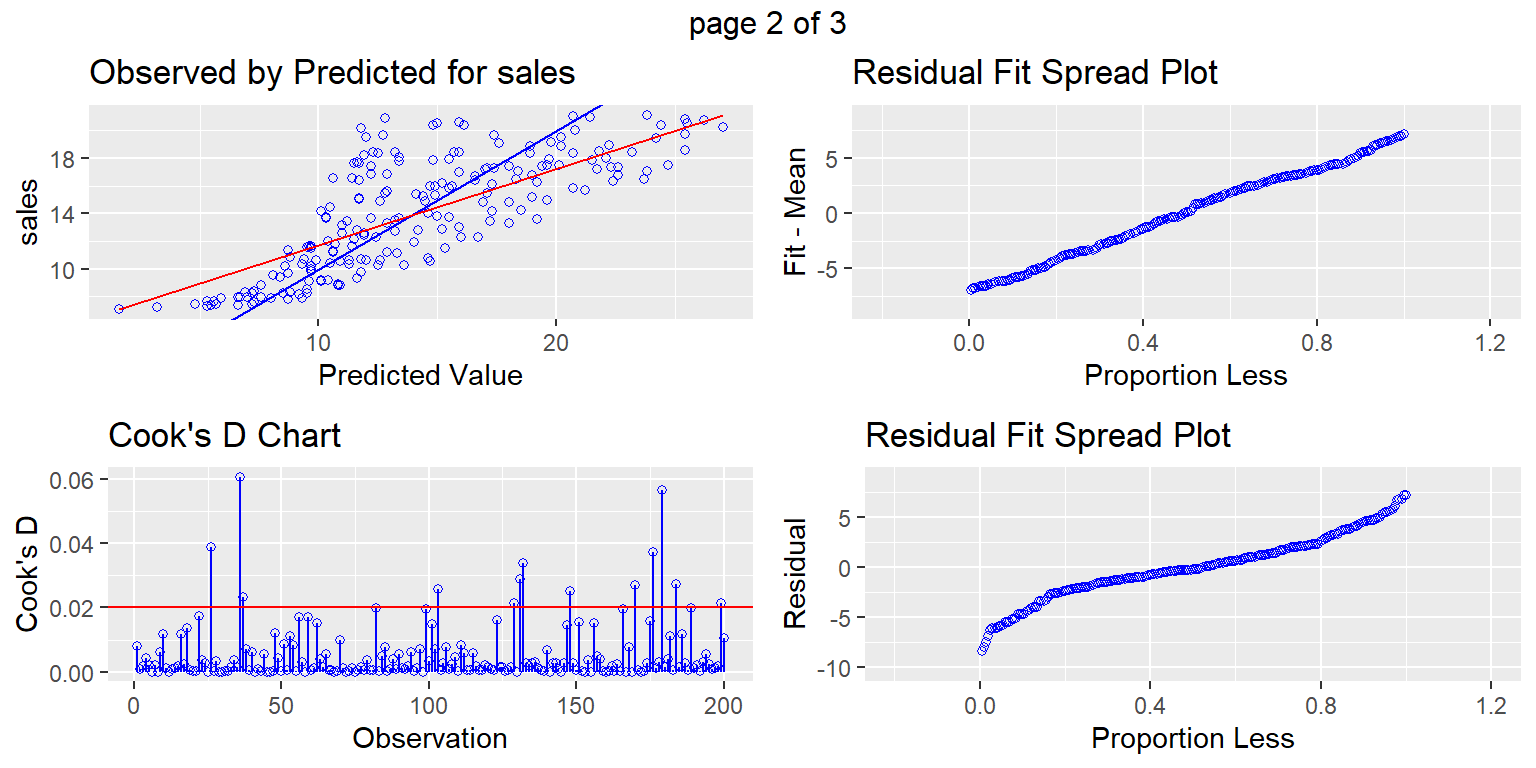
Regresión ponderada

Datos$Xprima=sqrt(Datos$TV)
fit2=lm(sales~Xprima, data=Datos)
summary(fit2)

## 
## Call:
## lm(formula = sales ~ Xprima, data = Datos)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -7.430 -1.953 -0.109  1.939  7.764 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    2.672      0.667     4.0  8.8e-05 ***
## Xprima         0.995      0.055    18.1  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 3.2 on 198 degrees of freedom
## Multiple R-squared:  0.623,  Adjusted R-squared:  0.621 
## F-statistic:  327 on 1 and 198 DF,  p-value: <2e-16

plot(fit2, 1)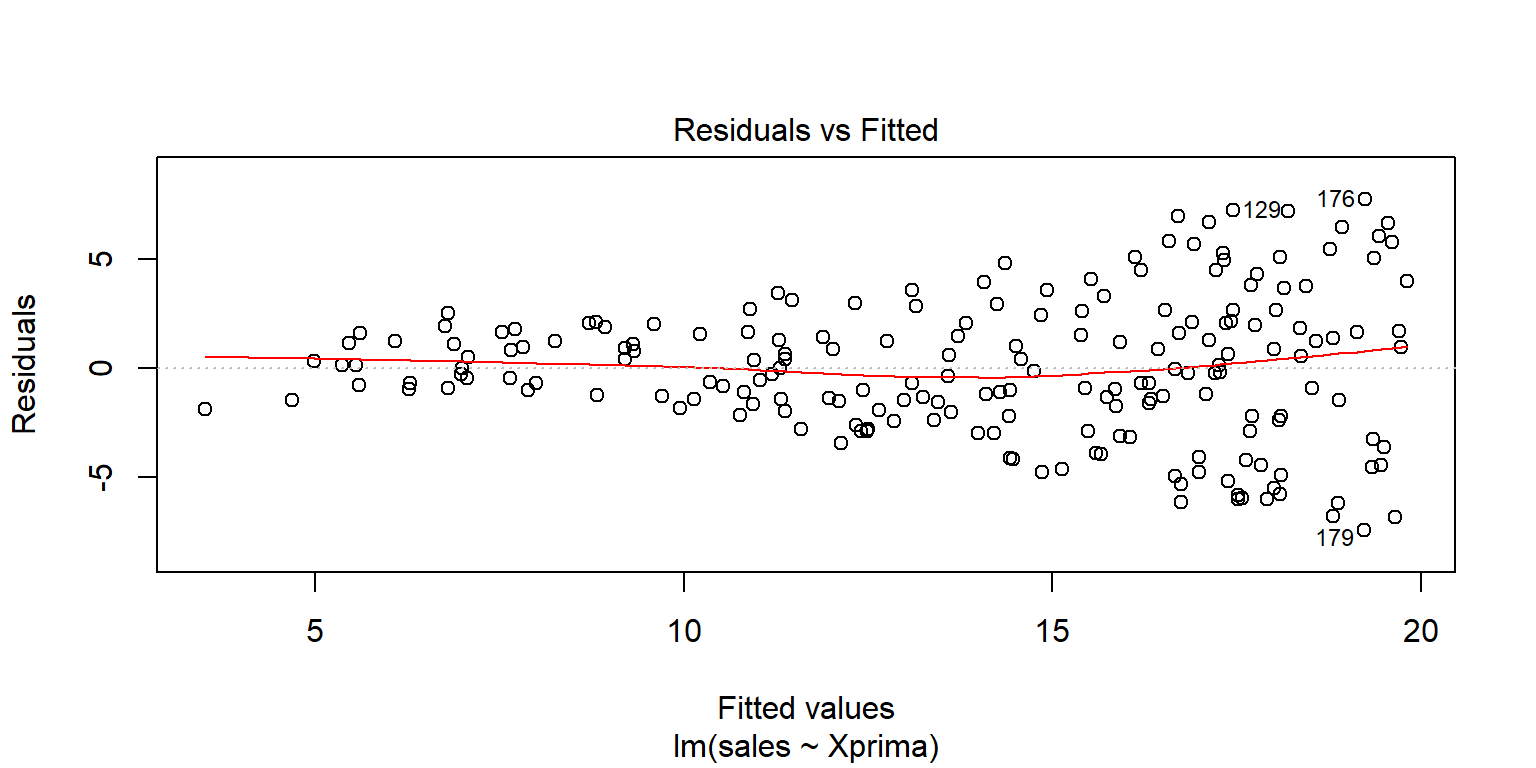

ggPoints(aes(x=Xprima,y=sales),method="lm", data=Datos,interactive=TRUE)

Datosfit2=augment(fit2)
head(Datosfit2)

## # A tibble: 6 x 9
##   sales Xprima .fitted .se.fit .resid    .hat .sigma  .cooksd .std.resid
##   <dbl>  <dbl>   <dbl>   <dbl>  <dbl>   <dbl>  <dbl>    <dbl>      <dbl>
## 1  22.1  15.2    17.8    0.308   4.33 0.00917   3.21 0.00848       1.35 
## 2  10.4   6.67    9.31   0.346   1.09 0.0116    3.22 0.000679      0.341
## 3   9.3   4.15    6.80   0.459   2.50 0.0205    3.22 0.00645       0.786
## 4  18.5  12.3    14.9    0.233   3.58 0.00524   3.21 0.00328       1.12 
## 5  12.9  13.4    16.1    0.253  -3.16 0.00623   3.21 0.00305      -0.986
## 6   7.2   2.95    5.61   0.518   1.59 0.0260    3.22 0.00336       0.502

ggPoints(aes(x=Xprima,y=.resid),smooth=FALSE, data=Datosfit2,interactive=TRUE)

Datosfit2$res2=Datosfit2$.resid^2
ggPoints(aes(x=Xprima,y=res2),smooth=FALSE, data=Datosfit2,interactive=TRUE)

fit2res=lm(res2~Xprima, data=Datosfit2)

summary(fit2res)

## 
## Call:
## lm(formula = res2 ~ Xprima, data = Datosfit2)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -18.87  -8.11  -1.28   4.61  41.28 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   -8.888      2.393   -3.71  0.00026 ***
## Xprima         1.675      0.197    8.49  4.9e-15 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 12 on 198 degrees of freedom
## Multiple R-squared:  0.267,  Adjusted R-squared:  0.263 
## F-statistic: 72.1 on 1 and 198 DF,  p-value: 4.87e-15

fit2res2=lm(res2~Xprima+I(Xprima^2), data=Datosfit2)

summary(fit2res2)

## 
## Call:
## lm(formula = res2 ~ Xprima + I(Xprima^2), data = Datosfit2)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -24.21  -6.21  -0.84   4.27  37.14 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   6.3385     4.6805    1.35  0.17721    
## Xprima       -1.9660     0.9910   -1.98  0.04866 *  
## I(Xprima^2)   0.1788     0.0478    3.74  0.00024 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 11 on 197 degrees of freedom
## Multiple R-squared:  0.316,  Adjusted R-squared:  0.309 
## F-statistic: 45.4 on 2 and 197 DF,  p-value: <2e-16

fit2res3=lm(res2~-1+Xprima+I(Xprima^2), data=Datosfit2)

summary(fit2res3)

## 
## Call:
## lm(formula = res2 ~ -1 + Xprima + I(Xprima^2), data = Datosfit2)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -23.04  -6.86   0.49   4.14  37.99 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## Xprima       -0.7014     0.3325   -2.11    0.036 *  
## I(Xprima^2)   0.1226     0.0237    5.17  5.6e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 11 on 198 degrees of freedom
## Multiple R-squared:  0.564,  Adjusted R-squared:  0.559 
## F-statistic:  128 on 2 and 198 DF,  p-value: <2e-16

Una opción es tomar como pesos \(w=1/(x)\)

fit2pond <- lm(sales~Xprima,weights = 1/( Xprima ), data=Datos)
summary(fit2pond)

## 
## Call:
## lm(formula = sales ~ Xprima, data = Datos, weights = 1/(Xprima))
## 
## Weighted Residuals:
##     Min      1Q  Median      3Q     Max 
## -1.9096 -0.6108 -0.0376  0.6791  1.8839 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   2.5013     0.3831    6.53  5.4e-10 ***
## Xprima        1.0104     0.0384   26.29  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.89 on 198 degrees of freedom
## Multiple R-squared:  0.777,  Adjusted R-squared:  0.776 
## F-statistic:  691 on 1 and 198 DF,  p-value: <2e-16

datonuevos= data.frame(Xprima=seq(0, 17, by=.2), sales=predict(fit2pond, newdata=data.frame(Xprima=seq(0, 17, by=.2) ) ))

datonuevos$TV=(datonuevos$Xprima)^(2)

ggplot(data=Datos, aes(x=TV,y=sales))+
  geom_point(colour="black")+
  geom_line(data= datonuevos, colour="green" )

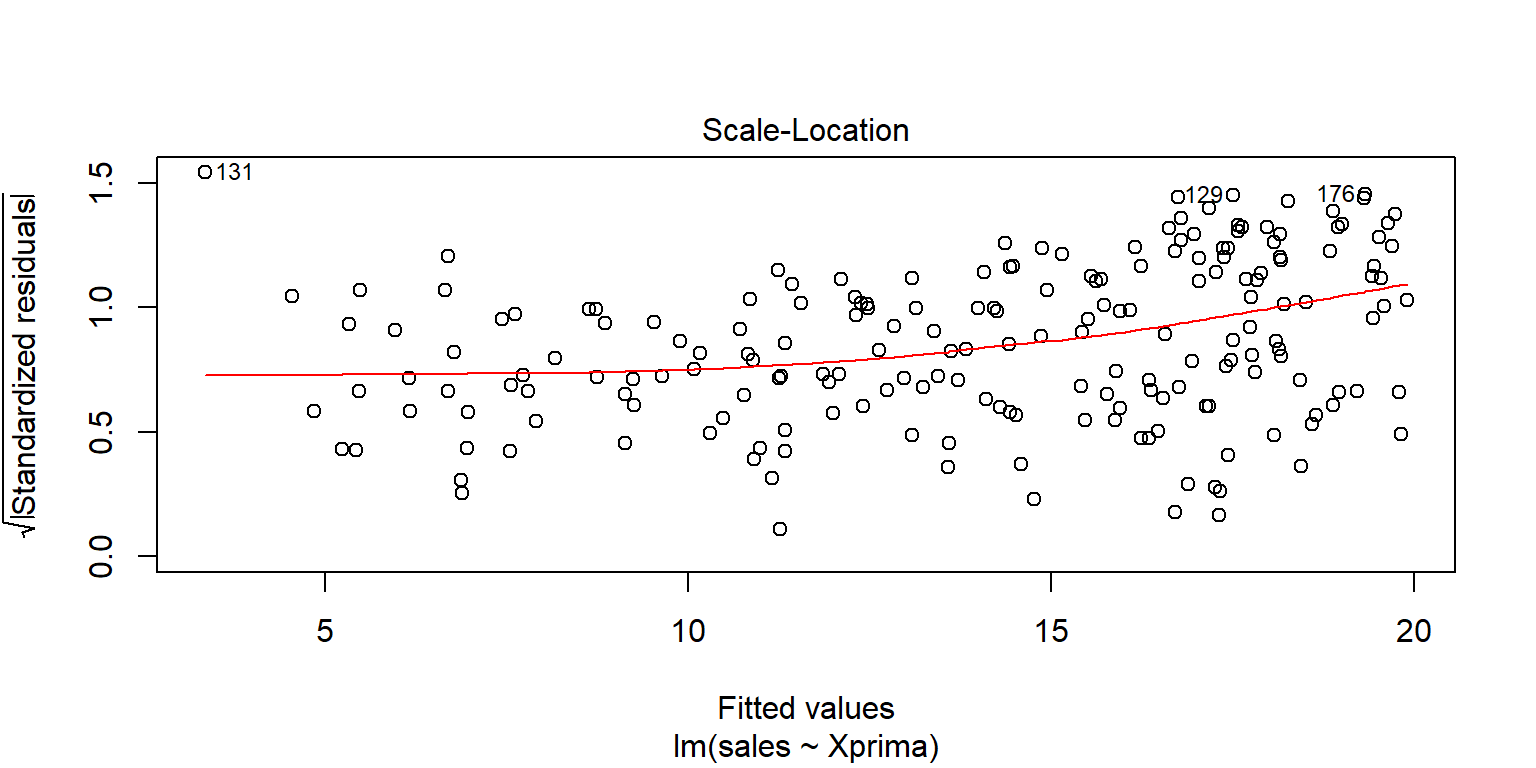
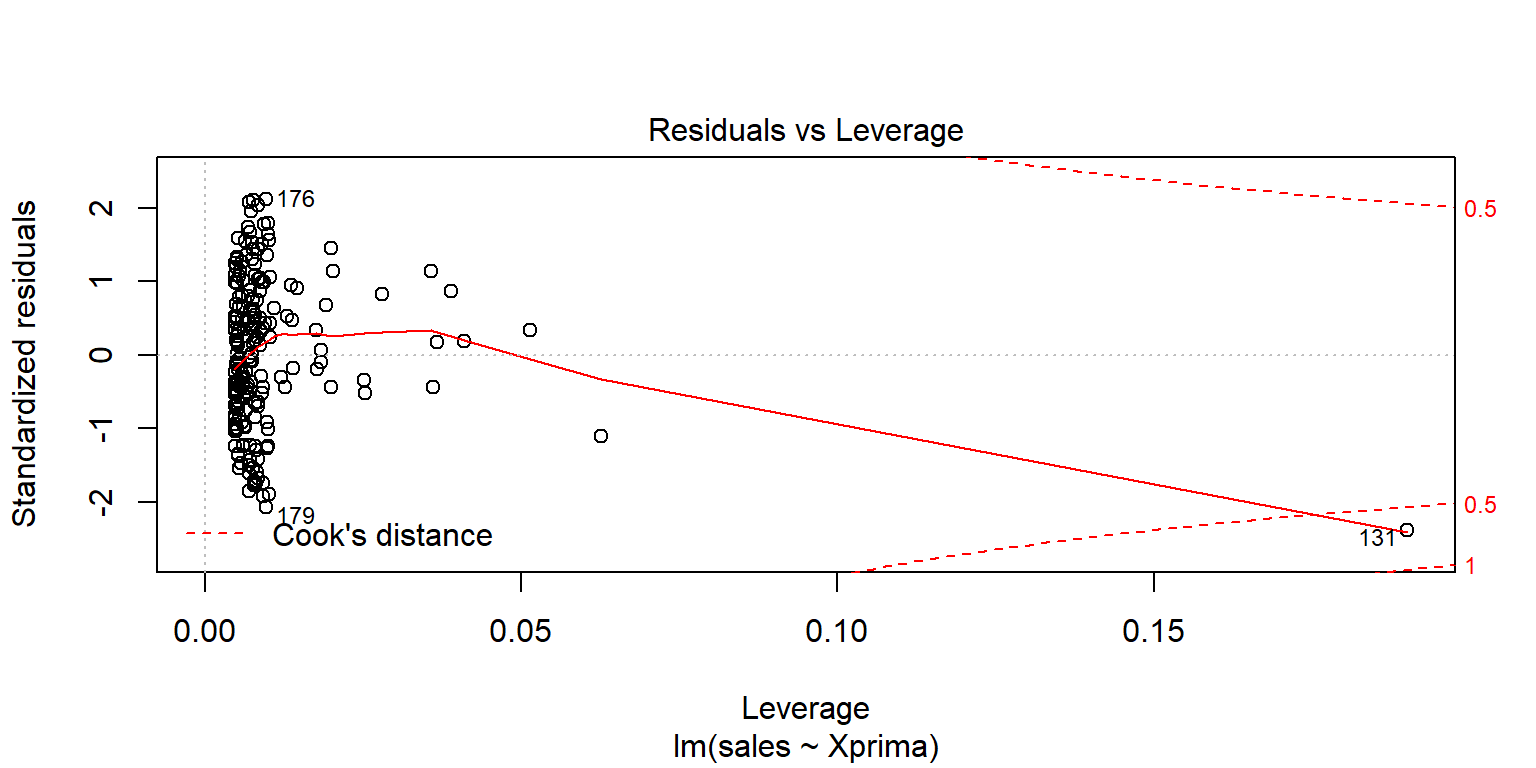
plot(fit2pond)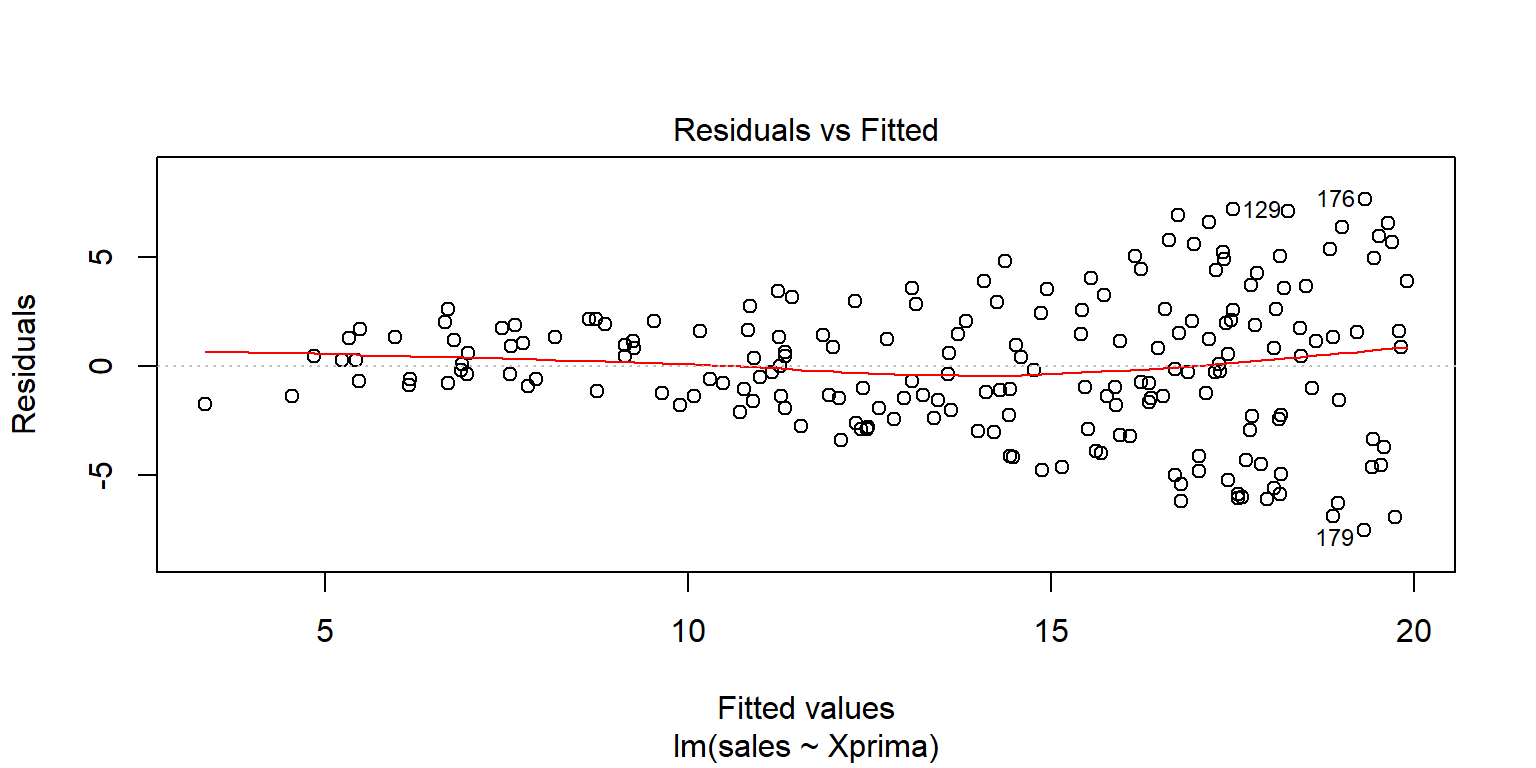

Datosfit2=augment(fit2pond)
head(Datosfit2)

## # A tibble: 6 x 10
##   sales Xprima X.weights. .fitted .se.fit .resid    .hat .sigma .cooksd
##   <dbl>  <dbl>      <dbl>   <dbl>   <dbl>  <dbl>   <dbl>  <dbl>   <dbl>
## 1  22.1  15.2      0.0659   17.8    0.310   4.27 0.00798  0.890 6.14e-3
## 2  10.4   6.67     0.150     9.24   0.202   1.16 0.00770  0.893 9.90e-4
## 3   9.3   4.15     0.241     6.69   0.256   2.61 0.0199   0.889 2.13e-2
## 4  18.5  12.3      0.0812   14.9    0.232   3.56 0.00549  0.890 3.60e-3
## 5  12.9  13.4      0.0744   16.1    0.260  -3.19 0.00634  0.891 3.05e-3
## 6   7.2   2.95     0.339     5.48   0.289   1.72 0.0357   0.890 2.42e-2
## # ... with 1 more variable: .std.resid <dbl>

normtest::jb.norm.test(Datosfit2$.std.resid)

## 
##  Jarque-Bera test for normality
## 
## data:  Datosfit2$.std.resid
## JB = 4, p-value = 0.08

nortest::lillie.test(Datosfit2$.std.resid)

## 
##  Lilliefors (Kolmogorov-Smirnov) normality test
## 
## data:  Datosfit2$.std.resid
## D = 0.04, p-value = 0.5

shapiro.test(Datosfit2$.std.resid)

## 
##  Shapiro-Wilk normality test
## 
## data:  Datosfit2$.std.resid
## W = 1, p-value = 0.09

fit2pond2 <- lm(sales~Xprima,weights = 1/(Xprima), data=Datos[-c(131),])
summary(fit2pond2)

## 
## Call:
## lm(formula = sales ~ Xprima, data = Datos[-c(131), ], weights = 1/(Xprima))
## 
## Weighted Residuals:
##     Min      1Q  Median      3Q     Max 
## -1.7953 -0.6135 -0.0396  0.6488  1.9298 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   2.9427     0.4205     7.0    4e-11 ***
## Xprima        0.9727     0.0411    23.7   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.88 on 197 degrees of freedom
## Multiple R-squared:  0.74,   Adjusted R-squared:  0.739 
## F-statistic:  561 on 1 and 197 DF,  p-value: <2e-16

plot(fit2pond2)

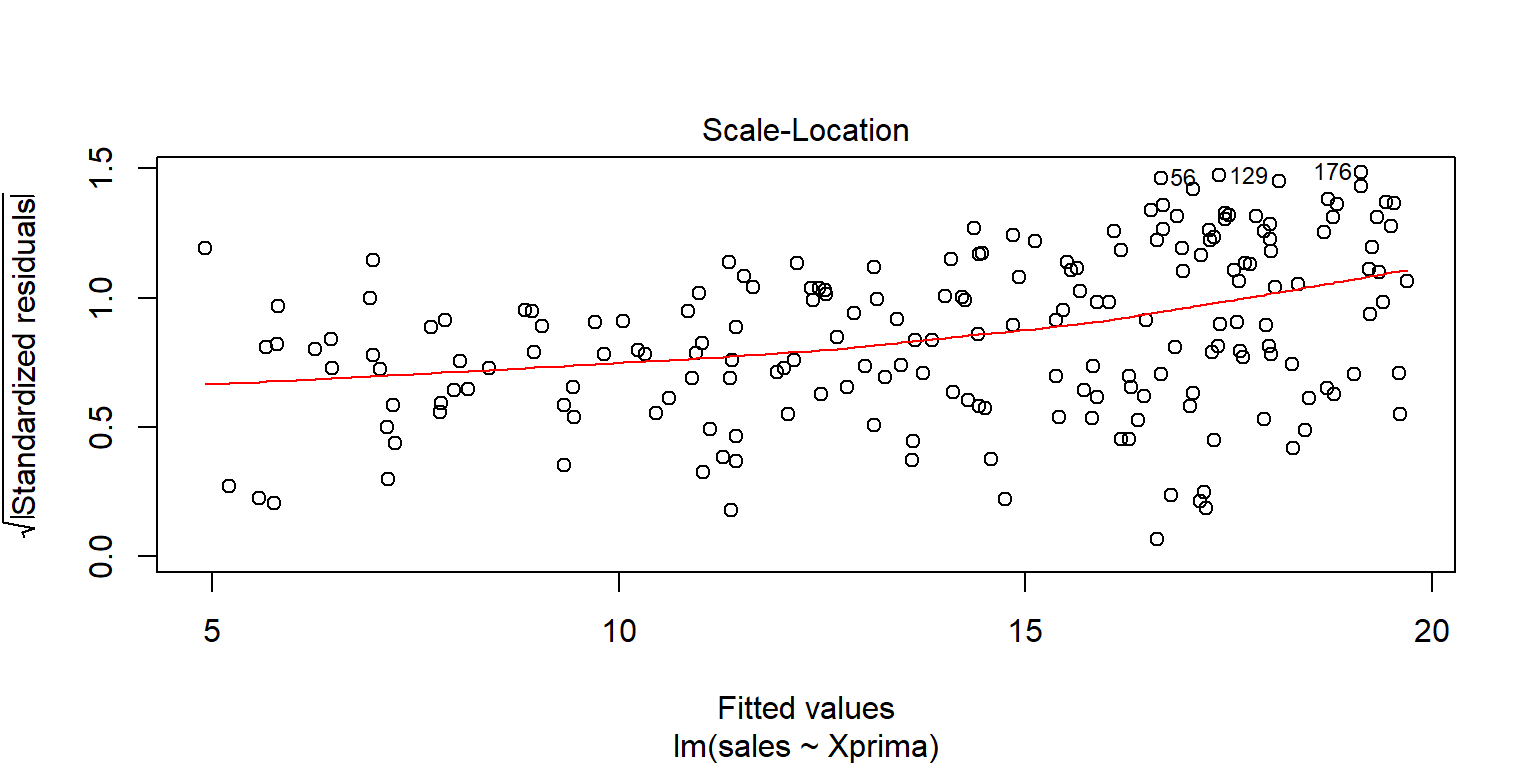
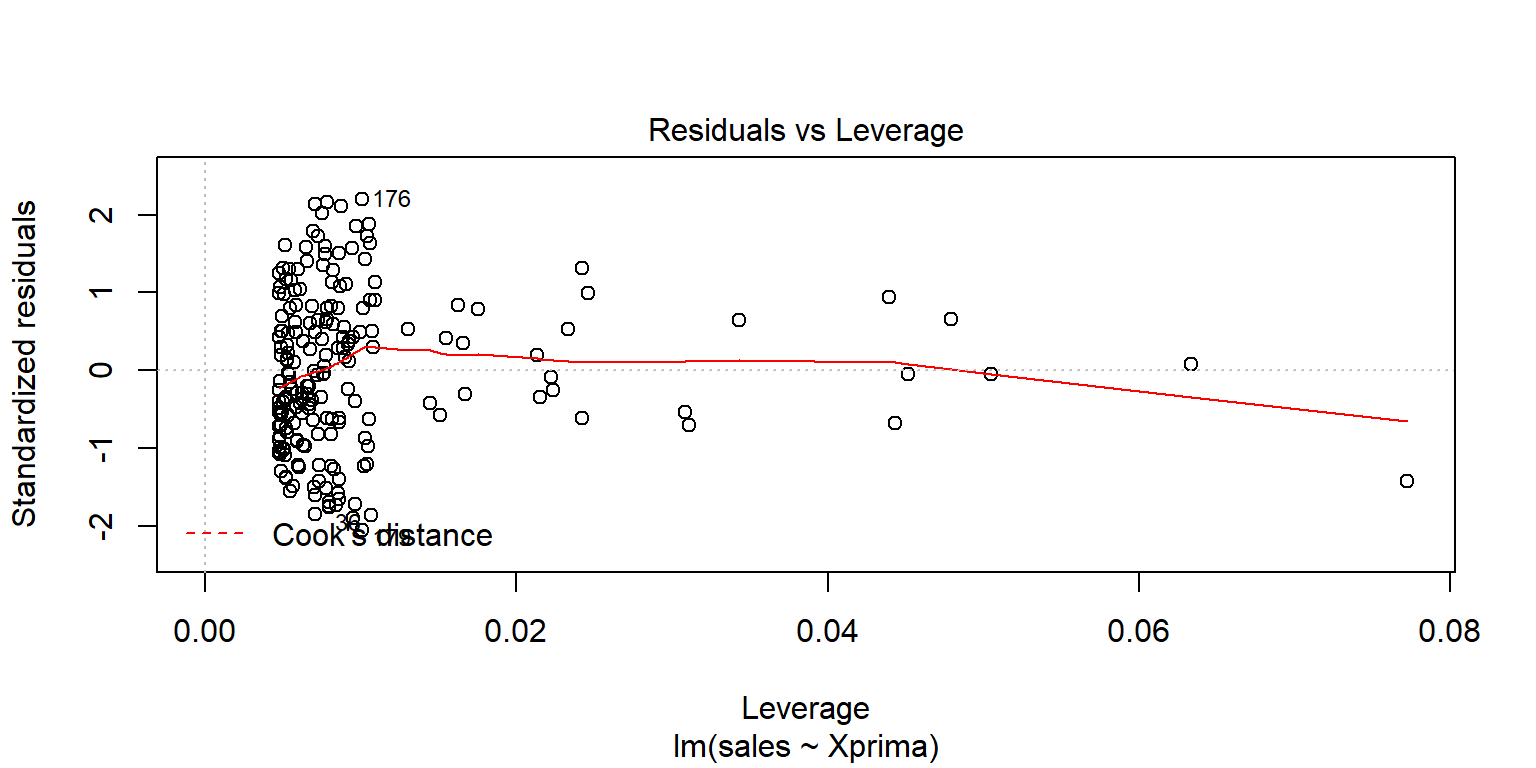
Datosfit2=augment(fit2pond2)
head(Datosfit2)

## # A tibble: 6 x 11
##   .rownames sales Xprima X.weights. .fitted .se.fit .resid    .hat .sigma
##   <chr>     <dbl>  <dbl>      <dbl>   <dbl>   <dbl>  <dbl>   <dbl>  <dbl>
## 1 1          22.1  15.2      0.0659   17.7    0.311  4.40  0.00823  0.879
## 2 2          10.4   6.67     0.150     9.43   0.214  0.969 0.00889  0.882
## 3 3           9.3   4.15     0.241     6.98   0.279  2.32  0.0242   0.879
## 4 4          18.5  12.3      0.0812   14.9    0.229  3.59  0.00550  0.880
## 5 5          12.9  13.4      0.0744   16.0    0.259 -3.12  0.00641  0.881
## 6 6           7.2   2.95     0.339     5.81   0.317  1.39  0.0439   0.881
## # ... with 2 more variables: .cooksd <dbl>, .std.resid <dbl>

normtest::jb.norm.test(Datosfit2$.std.resid)

## 
##  Jarque-Bera test for normality
## 
## data:  Datosfit2$.std.resid
## JB = 5, p-value = 0.06

nortest::lillie.test(Datosfit2$.std.resid)

## 
##  Lilliefors (Kolmogorov-Smirnov) normality test
## 
## data:  Datosfit2$.std.resid
## D = 0.05, p-value = 0.2

shapiro.test(Datosfit2$.std.resid)

## 
##  Shapiro-Wilk normality test
## 
## data:  Datosfit2$.std.resid
## W = 1, p-value = 0.03

datonuevos= data.frame(Xprima=seq(0, 17, by=.2), sales=predict(fit2pond2, newdata=data.frame(Xprima=seq(0, 17, by=.2) ) ))

datonuevosold= data.frame(Xprima=seq(0, 17, by=.2), sales=predict(fit2pond, newdata=data.frame(Xprima=seq(0, 17, by=.2) ) ))

datonuevos$TV=(datonuevos$Xprima)^(2)
datonuevosold$TV=(datonuevos$Xprima)^(2)

ggplot(data=Datos, aes(x=TV,y=sales))+
  geom_point(colour="black")+
  geom_line(data= datonuevos, colour="green" )+
geom_line(data= datonuevosold, colour="red" )

ggplot(data=Datos, aes(x=Xprima,y=sales))+
  geom_point(colour="black")+
  geom_line(data= datonuevos, colour="green" )+
geom_line(data= datonuevosold, colour="red" )

Otra opción es tomar como pesos \(w=1/(6.33-1.96x+.18x^2)\)

fit2pondv2 <- lm(sales~Xprima,weights = 1/(6.33-1.96*Xprima+.18*Xprima^2), data=Datos)
summary(fit2pondv2)

## 
## Call:
## lm(formula = sales ~ Xprima, data = Datos, weights = 1/(6.33 - 
##     1.96 * Xprima + 0.18 * Xprima^2))
## 
## Weighted Residuals:
##     Min      1Q  Median      3Q     Max 
## -1.7604 -0.8913 -0.0963  0.7780  1.9610 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   3.3205     0.3376    9.83   <2e-16 ***
## Xprima        0.9345     0.0406   23.00   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1 on 198 degrees of freedom
## Multiple R-squared:  0.728,  Adjusted R-squared:  0.726 
## F-statistic:  529 on 1 and 198 DF,  p-value: <2e-16

plot(fit2pondv2)

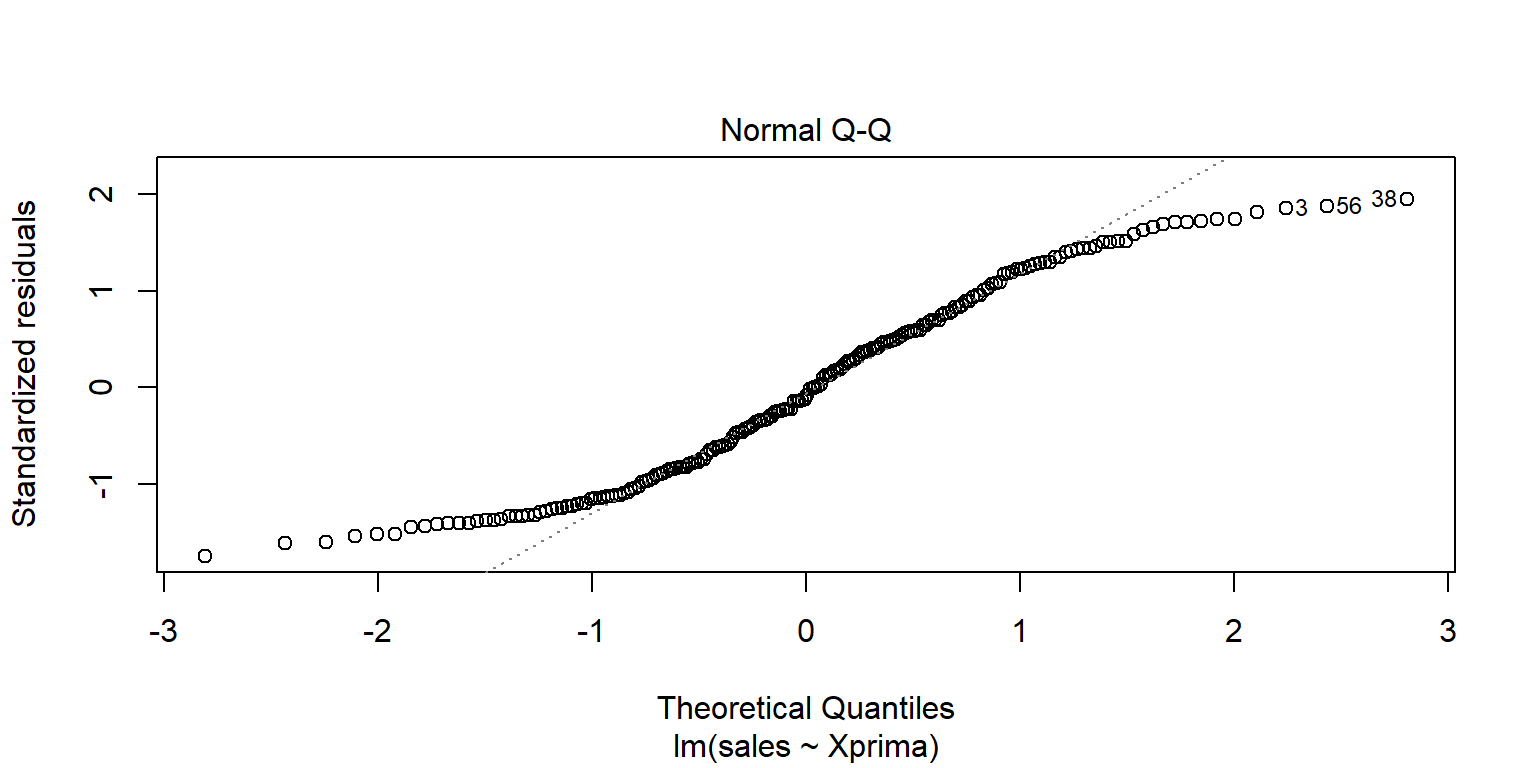
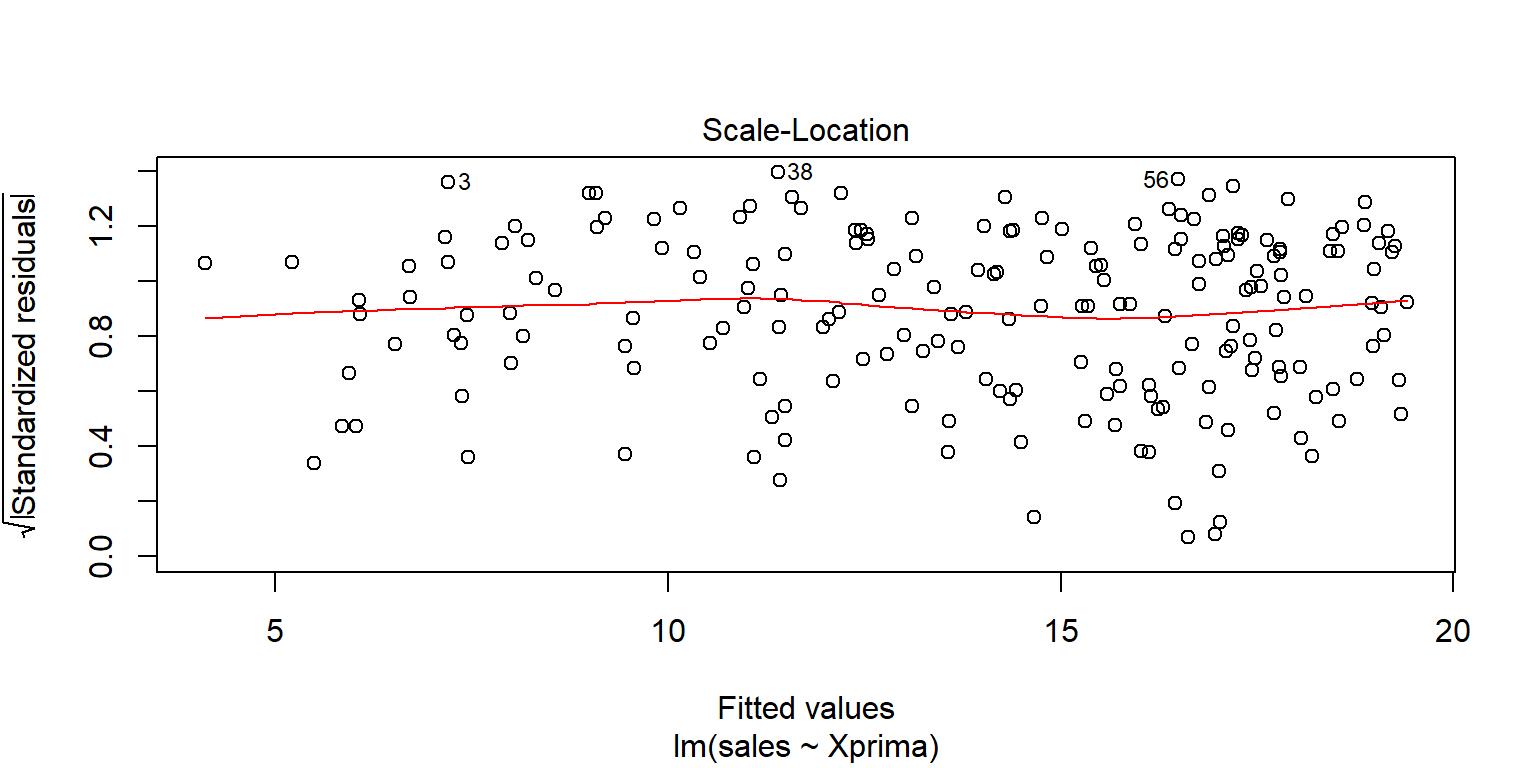
Datosfit2=augment(fit2pondv2)
head(Datosfit2)

## # A tibble: 6 x 10
##   sales Xprima X.weights. .fitted .se.fit .resid    .hat .sigma .cooksd
##   <dbl>  <dbl>      <dbl>   <dbl>   <dbl>  <dbl>   <dbl>  <dbl>   <dbl>
## 1  22.1  15.2      0.0555   17.5    0.342  4.60  0.00635   1.01 0.00370
## 2  10.4   6.67     0.790     9.55   0.147  0.845 0.0168    1.01 0.00479
## 3   9.3   4.15     0.771     7.20   0.198  2.10  0.0297    1.00 0.0526 
## 4  18.5  12.3      0.106    14.8    0.241  3.68  0.00601   1.01 0.00425
## 5  12.9  13.4      0.0799   15.9    0.280 -2.99  0.00612   1.01 0.00216
## 6   7.2   2.95     0.473     6.08   0.235  1.12  0.0255    1.01 0.00783
## # ... with 1 more variable: .std.resid <dbl>

normtest::jb.norm.test(Datosfit2$.std.resid)

## 
##  Jarque-Bera test for normality
## 
## data:  Datosfit2$.std.resid
## JB = 12, p-value = 0.008

¿Quizás transformar Y?