Regresión lineal simple

Análisis de residuales y verificación de supuestos del modelo.

En el modelo de regresión lineal simple se hacen principalmente los siguientes supuestos:

Relación lineal entre la variable \(X\) y \(Y\).
Errores independientes
Errores con la misma varianza (homocedasticidad)
Distribución normal de los errores

Otros problemas potenciales que se pueden encontrar son outliers (generalmente en la variable \(Y\)) y valores extremos en la variable \(X\), en ambos casos se debe analizar si estos son influyentes.

La revisión de la mayoría de estos supuestos se realiza de forma gráfica y usando los residuales (o errores estimados) o adaptaciones de éstos.

Relación lineal entre la variable \(X\) y \(Y\).

Esta revisión se puede realizar en la regresión lineal simple directamente observando el scatterplot de los datos \(X\) y \(Y\).

Ejemplo de la compañía Toluca, equipo de reemplazo de refrigeración.

\(X=\) tamaño del lote.

\(Y=\) horas de trabajo.

library(ALSM)


Datos=TolucaCompany
head(Datos)

##    x   y
## 1 80 399
## 2 30 121
## 3 50 221
## 4 90 376
## 5 70 361
## 6 60 224

str(Datos)

## 'data.frame':    25 obs. of  2 variables:
##  $ x: int  80 30 50 90 70 60 120 80 100 50 ...
##  $ y: int  399 121 221 376 361 224 546 352 353 157 ...

require(ggplot2)
require(ggiraph)
require(ggiraphExtra)
ggPoints(aes(x=x,y=y),method="lm", data=Datos,interactive=TRUE)

Sin embargo, es muy común usar también la gráfica de los residuales \(y_i-\hat{y}_i\) contra los valores ajustados \(\hat{y}_i\). El objeto obtenido al usar la función lm en R tiene preestablecidas varias gráficas que sirven para los análisis.

fit1=lm(y~x, data=Datos)
summary(fit1)

## 
## Call:
## lm(formula = y ~ x, data = Datos)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -83.88 -34.09  -5.98  38.83 103.53 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   62.366     26.177    2.38    0.026 *  
## x              3.570      0.347   10.29  4.4e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 49 on 23 degrees of freedom
## Multiple R-squared:  0.822,  Adjusted R-squared:  0.814 
## F-statistic:  106 on 1 and 23 DF,  p-value: 4.45e-10

plot(fit1, 1)

En este caso, lo ideal sería que los residuales no muestren ningún patrón con respecto a no seguir en promedio una línea horizontal con media cero. En algunos casos, se pueden observar patrones en esta gráfica que indican que la relación no es lineal, además también se podría observa un patrón sobre la variabilidad de los residuales.

Opciones para arreglar la linealidad son considerar transformaciones a los datos, ya sea a la variable \(X\), a la variable \(Y\) o ambas. Por ejemplo usando transformaciones tipo Box-Cox en \(Y\) (librería car, función boxCox) o en la variable \(X\) (funcion boxTidwell).

Homocedasticidad

Se usa la gráfica de los residuales estandarizados contra los valores ajustados \(\hat{y}_i\). Se busca que los errores se distribuyan sin ningún patrón

plot(fit1, 3)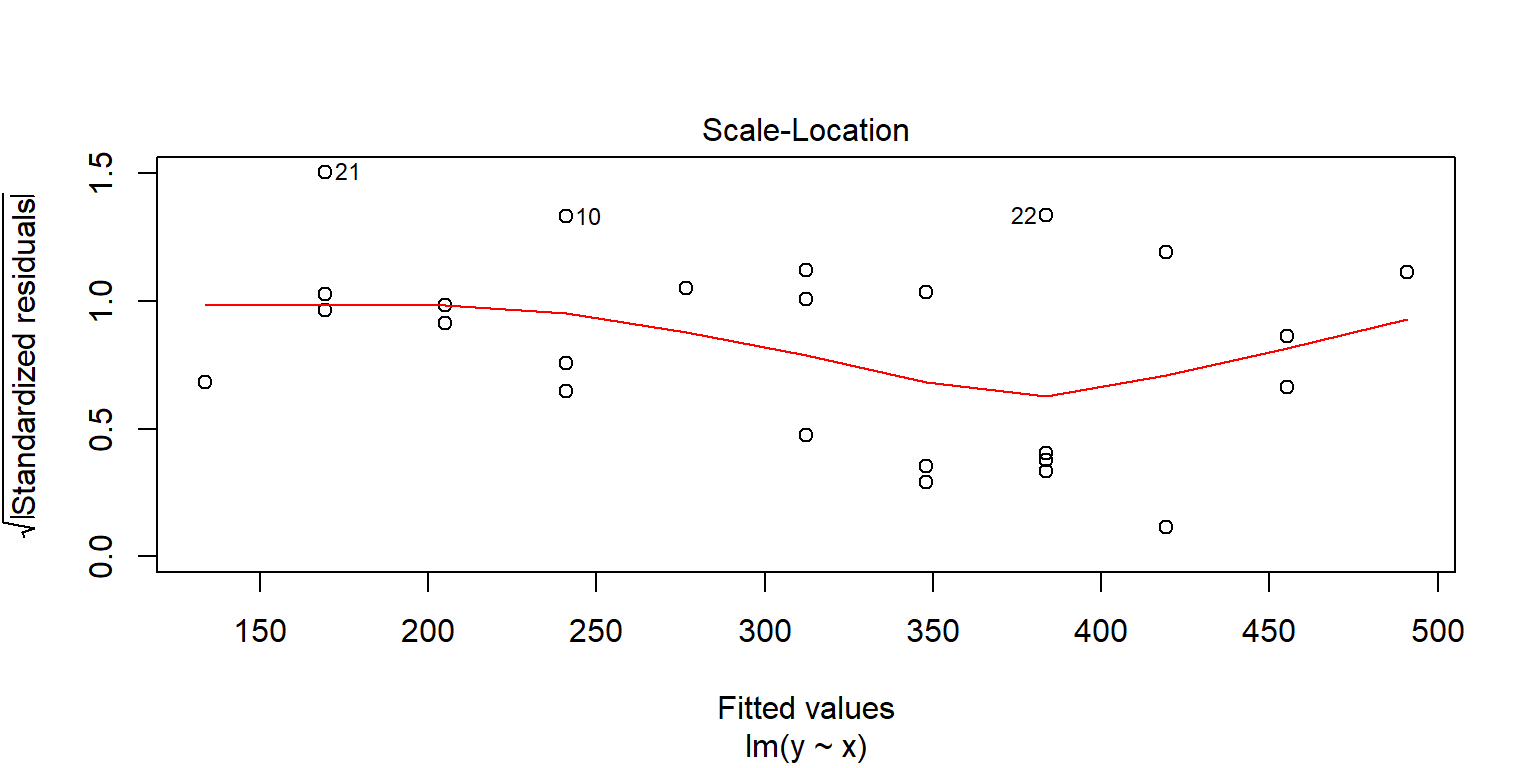

Existen algunas pruebas que pueden ayudar.

Breush Pagan Test. \(H_0\): La varianza de los residuales no depende de las variables en el modelo, es decir, es constante.

library(lmtest)
lmtest::bptest(fit1)

## 
##  studentized Breusch-Pagan test
## 
## data:  fit1
## BP = 1, df = 1, p-value = 0.3

Score Test

library(car)
car::ncvTest(fit1)

## Non-constant Variance Score Test 
## Variance formula: ~ fitted.values 
## Chisquare = 0.82, Df = 1, p = 0.4

Errores independientes

library(broom)
Datosfit1=augment(fit1)
head(Datosfit1)

## # A tibble: 6 x 9
##       y     x .fitted .se.fit .resid   .hat .sigma  .cooksd .std.resid
##   <int> <int>   <dbl>   <dbl>  <dbl>  <dbl>  <dbl>    <dbl>      <dbl>
## 1   399    80    348.   10.4   51.0  0.0451   48.7 0.0270        1.07 
## 2   121    30    169.   17.0  -48.5  0.121    48.7 0.0770       -1.06 
## 3   221    50    241.   12.0  -19.9  0.0602   49.7 0.00565      -0.420
## 4   376    90    384.   12.0   -7.68 0.0602   49.9 0.000844     -0.162
## 5   361    70    312.    9.76  48.7  0.04     48.8 0.0216        1.02 
## 6   224    60    277.   10.4  -52.6  0.0451   48.6 0.0286       -1.10

acf(Datosfit1$.std.resid)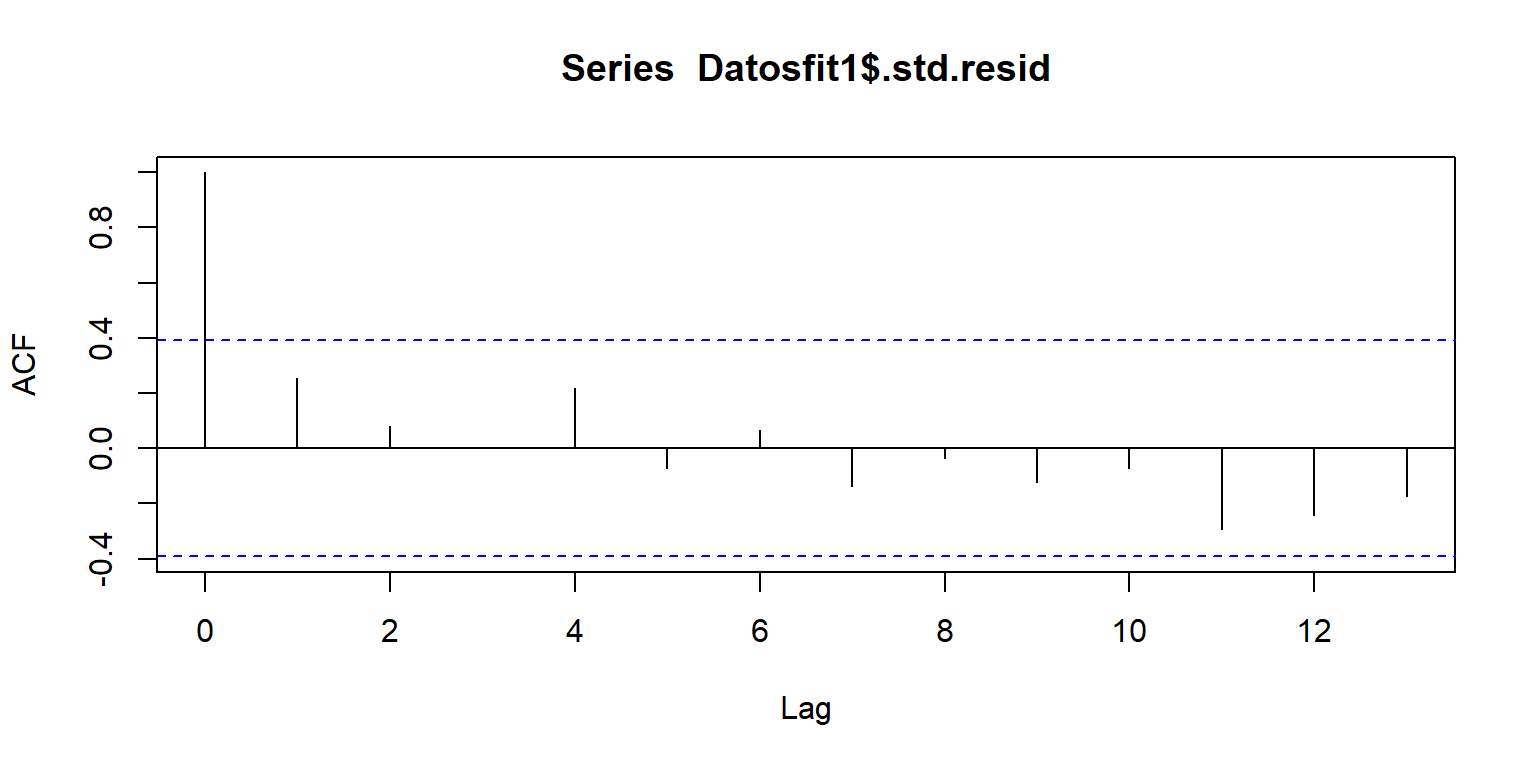

Algunas pruebas

Prueba de rachas. \(H_0\) los datos son aleatorios

library(lawstat)
lawstat::runs.test(Datosfit1$.std.resid)

## 
##  Runs Test - Two sided
## 
## data:  Datosfit1$.std.resid
## Standardized Runs Statistic = -1, p-value = 0.3

library(randtests)
randtests::runs.test(Datosfit1$.std.resid)

## 
##  Runs Test
## 
## data:  Datosfit1$.std.resid
## statistic = -0.8, runs = 11, n1 = 12, n2 = 12, n = 24, p-value = 0.4
## alternative hypothesis: nonrandomness

Prueba Durbin-Watson. \(H_0\) los errores no están autocorrelacionados.

lmtest::dwtest(fit1)

## 
##  Durbin-Watson test
## 
## data:  fit1
## DW = 1, p-value = 0.08
## alternative hypothesis: true autocorrelation is greater than 0

Normalidad de los residuales

Por lo general se revisa con una qq-plot de los errores estandarizados. lm tiene una gráfica directa. Se desea que los puntos estén sobre la línea recta dibujada.

plot(fit1, 2)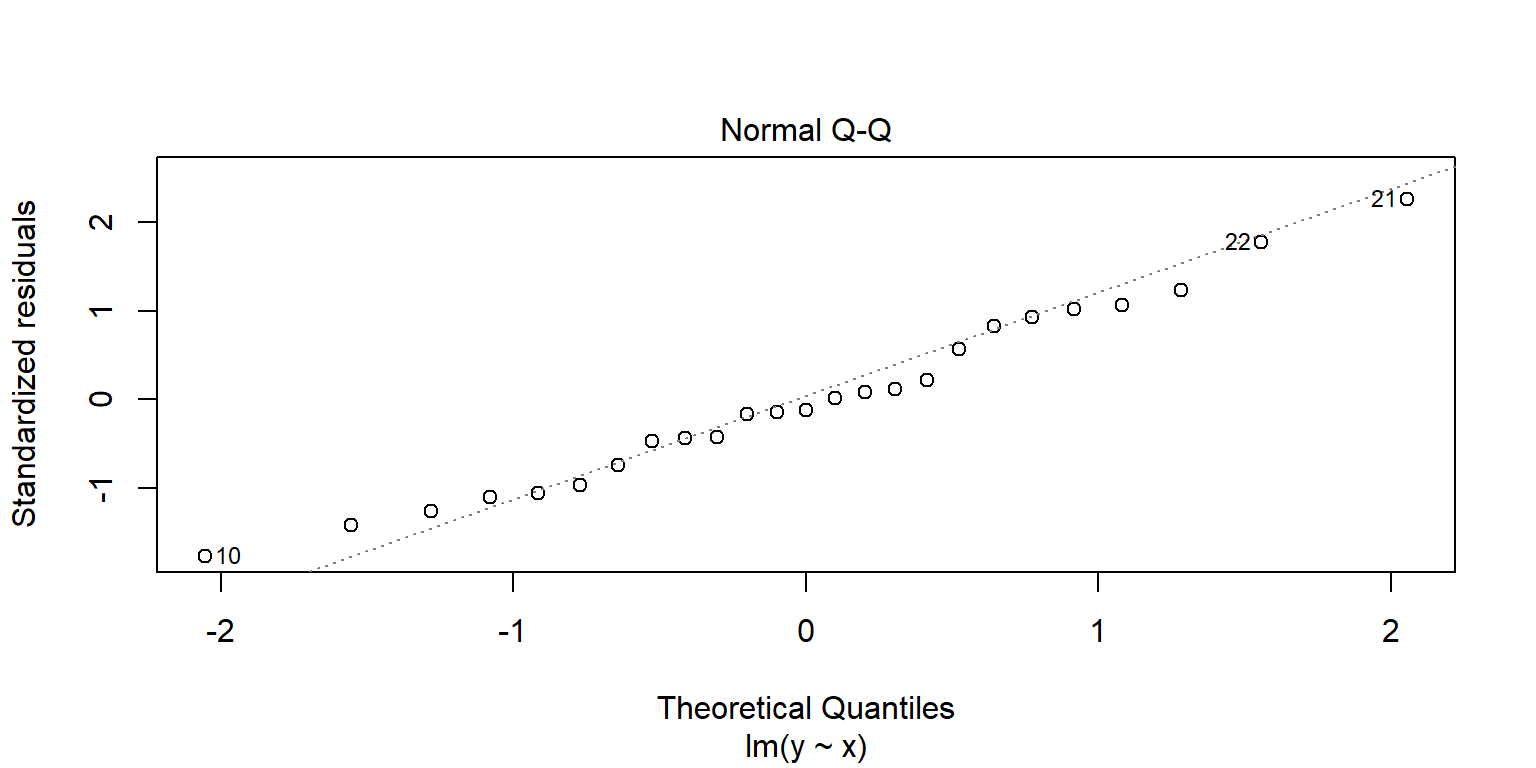

Algunos test. \(H_0\): los valores son normales.

shapiro.test(Datosfit1$.std.resid)

## 
##  Shapiro-Wilk normality test
## 
## data:  Datosfit1$.std.resid
## W = 1, p-value = 0.9

library(nortest)

nortest::lillie.test(Datosfit1$.std.resid)

## 
##  Lilliefors (Kolmogorov-Smirnov) normality test
## 
## data:  Datosfit1$.std.resid
## D = 0.1, p-value = 0.8

library(normtest)
normtest::jb.norm.test(Datosfit1$.std.resid)

## 
##  Jarque-Bera test for normality
## 
## data:  Datosfit1$.std.resid
## JB = 0.7, p-value = 0.6

Outliers y valores influyentes

Outliers se pueden observar con la gráfica de residuales estandarizados. En general, se consideran que los residuales más grandes de 2 (3) podrían ser outliers.
Existen algunas observaciones cuyo valor es extremo en la variable predictora. Se recomienda revisar la estadística leverage. En general, si esta estadística es superior a \(4/n\) se dice que tiene un valor muy grande en \(X\).
Las observaciones influyentes son aquellas que al eliminarlas pueden alterar los resultados de la regresión. Una metrica para analizar estos valores se conoce como Cook’s distance. Una regla empírica es considerar como observación influyente si esta distancia excede \(4/(n-2)\).

En R, existe una gráfica que resume lo anterior

plot(fit1, 5)

plot(fit1, 4)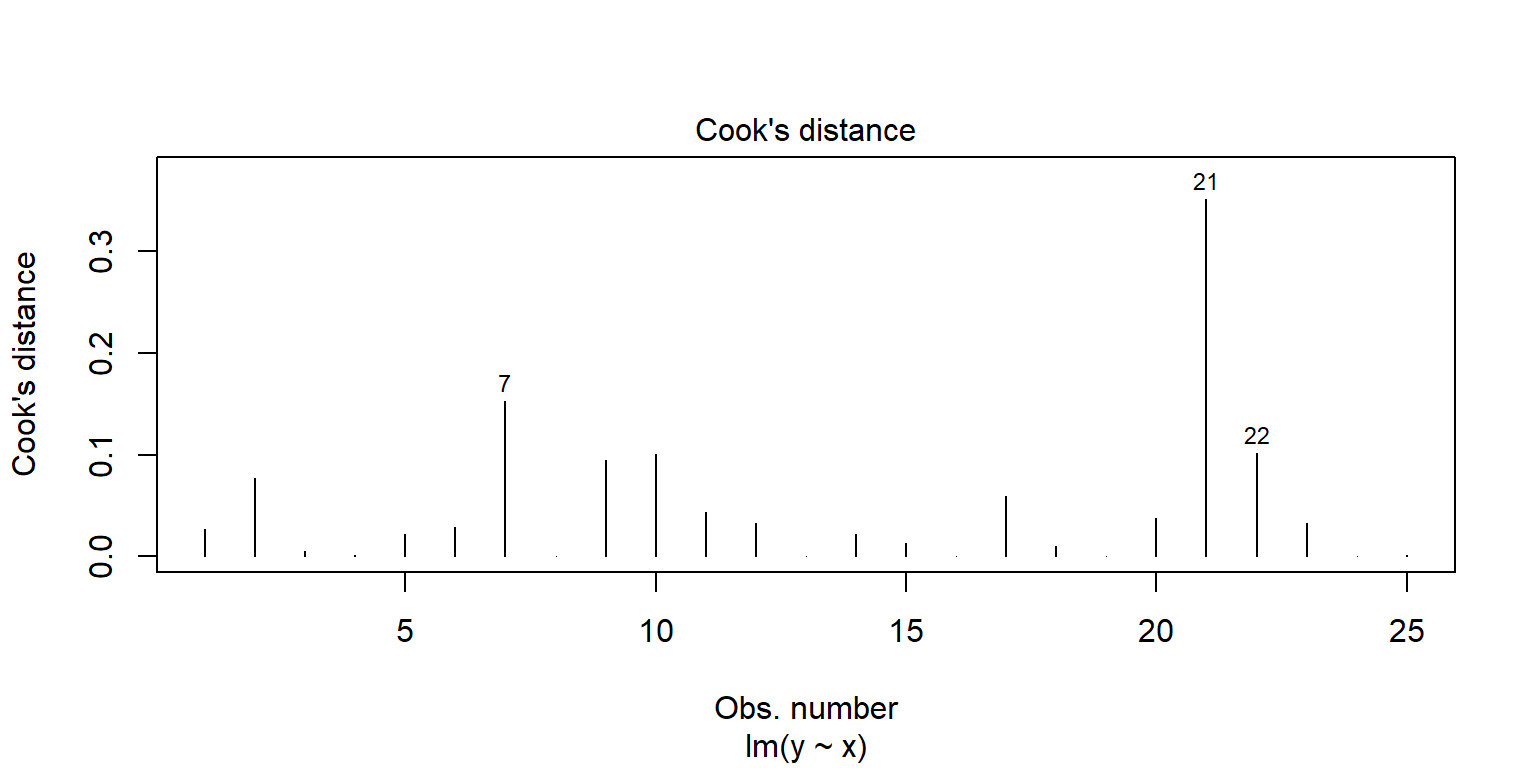

Si se observan casos que están en los extremos inferior o superior derecho, se deben revisar. Una opción es ajustar un modelo eliminando esos casos y ver qué tanto se modifican las conclusiones.