Presentación.
Modelos Lineales
Gonzalo Pérez
27 de enero de 2020
Características generales del curso
Profesor: Gonzalo Pérez (cubículo 212, Departamento de Matemáticas, gonzalo.perez@ciencias.unam.mx).
Ayudante: Por definir.
Horario: lunes a viernes de 20 a 21 hrs.
Salón: O125
Evaluación
Tres examenes parciales, dos de ellos son tarea-examen. Cada examen tiene el mismo valor: 1/3 de la calificación.
El examen teórico será antecedido por una tarea. La tarea se entregará de forma opcional. Se podrá entregar por parejas y SÓLO con calificación mayor o igual a 9 tendrá un valor de un punto adicional al examen parcial correspondiente.
Como parte de las tarea-examen, el alumno deberá entregar un reporte escrito y realizar una presentación de los resultados al grupo, así como una breve descripción de los paquetes estadísticos usados. Las tarea-examen se realizarán en equipos, el número de integrantes se definirá de acuerdo con el número de alumnos inscritos.
Para aprobar el curso es necesario aprobar el examen teórico.
Notas sobre la evaluación
Se podrá reponer el examen teórico renunciando a la calificación previa obtenida.
Habrá un exámen final que podrá presentarse de forma opcional renunciando a la calificación final previamente obtenida.
La calificación se redondea al entero más cercano a partir de 6, de otra forma la calificación es no aprobatoria.
Se califica con NP en actas únicamente cuando el número de exámenes presentados es menor a 2.
Temas por cubrir en el curso.
- Introducción
- Descripción de los modelos lineales.
- Uso de los modelos lineales generalizados (MLG).
- Propiedades de la familia exponencial.
- El modelo lineal
- Ajuste por mínimos cuadrados.
- Rango completo.
- Rango incompleto.
- Funciones estimables y sus propiedades.
- Ajuste por mínimos cuadrados.
- El modelo lineal como un MLG con variable de respuesta con distribución normal.
- Estimadores por máxima verosimilitud.
- Intervalos de confianza y pruebas de hipótesis.
- Modelos con variables explicativas discretas y continuas
- ANOVA
- ANCOVA
- Modelos lineales generalizados cuya variable dependiente es un conteo.
- Regresión Poisson.
- Estimación de parámetros e interpretación.
- Modelos lineales generalizados cuya variable dependiente es discreta.
- Regresión logística.
- Estimación de parámetros e interpretación.
- Selección de modelos.
- Otros modelos para respuestas binarias: probit y log-log
- Modelos para respuestas con más de dos categorías.
- Regresión logística.
- El caso general de un MLG.
Referencias básicas
Agresti, A. (2015). Foundations of linear and generalized linear models. Wiley.
Dobson, A. y Barnett, A. (2018). An introduction to generalized linear models. CRC Press.
Faraway, J. (2016). Extending the Linear Model with R. Generalized Linear, Mixed Effects and Nonparametric Regression Models. CRC Press.
Fox, J. (2015). Applied Regression Analysis and Generalized Linear Models. Sage Publications, Thousand Oaks, California.
Searle, S.R. (1971). Linear Models. Linear Models. Wiley.
Seber, G.A.F. y Lee, A. (2003). Linear Regression Analysis. Wiley.
¿De qué trata el tema de regresión lineal simple?
Tenemos acceso a un conjunto de \(n\) observaciones
\[z_1, ..., z_n.\]
Cada observación es un vector de dos variables, es decir,
\(z_i=(y_i, x_i), i=1,...,n\).
Por ejemplo. Supongamos que se tiene acceso a un conjunto de 32 datos medidos en automóviles; en donde \(y_i\) corresponde a las millas por galón que recorre el auto \(i-ésimo\) y \(x_i\) a su peso. Supongamos que queremos comprar un auto, pero quisieramos saber si es posible reducir costos en gasolina a partir de las características del automóvil. Algunas preguntas que se pueden derivar de estos datos son:
- ¿A mayor peso del auto se gasta más gasolina? ¿En qué magnitud?
- ¿La relacion entre el peso del auto y el gasto de gasolina es lineal?
Veamos qué nos dicen los datos!
str(mtcars)## 'data.frame': 32 obs. of 11 variables:
## $ mpg : num 21 21 22.8 21.4 18.7 18.1 14.3 24.4 22.8 19.2 ...
## $ cyl : num 6 6 4 6 8 6 8 4 4 6 ...
## $ disp: num 160 160 108 258 360 ...
## $ hp : num 110 110 93 110 175 105 245 62 95 123 ...
## $ drat: num 3.9 3.9 3.85 3.08 3.15 2.76 3.21 3.69 3.92 3.92 ...
## $ wt : num 2.62 2.88 2.32 3.21 3.44 ...
## $ qsec: num 16.5 17 18.6 19.4 17 ...
## $ vs : num 0 0 1 1 0 1 0 1 1 1 ...
## $ am : num 1 1 1 0 0 0 0 0 0 0 ...
## $ gear: num 4 4 4 3 3 3 3 4 4 4 ...
## $ carb: num 4 4 1 1 2 1 4 2 2 4 ...require(ggplot2)
require(ggiraph)
require(ggiraphExtra)
ggPoints(aes(x=wt,y=mpg),data=mtcars,method="lm",interactive=TRUE)La linea azul corresponde a una recta parametrizada como
\[Y=\beta_1+\beta_2 X\]
Preguntas a resolver durante el curso:
- ¿Cómo estimar los parámetros de la regresión lineal, \(\beta_1, \beta_2\)?
- ¿Cómo verificar que realmente a mayor peso mayor gasto de gasolina?
- ¿Cómo interpretar los parámetros? ¿Qué propiedades tienen?
En general se puede observar lo siguiente en cuanto a la interpretación de la recta:
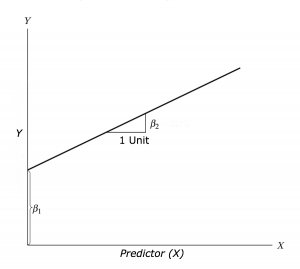
¿Qué herramientas computacionales podemos usar?
Python
Sólo se mostrarán funciones básicas.
import numpy as np
import statsmodels.api as sm
import statsmodels.formula.api as smf
model = smf.ols('mpg ~ wt', data = r.mtcars).fit()
print(model.summary())## OLS Regression Results
## ==============================================================================
## Dep. Variable: mpg R-squared: 0.753
## Model: OLS Adj. R-squared: 0.745
## Method: Least Squares F-statistic: 91.38
## Date: Sun, 26 Jan 2020 Prob (F-statistic): 1.29e-10
## Time: 22:40:14 Log-Likelihood: -80.015
## No. Observations: 32 AIC: 164.0
## Df Residuals: 30 BIC: 167.0
## Df Model: 1
## Covariance Type: nonrobust
## ==============================================================================
## coef std err t P>|t| [0.025 0.975]
## ------------------------------------------------------------------------------
## Intercept 37.2851 1.878 19.858 0.000 33.450 41.120
## wt -5.3445 0.559 -9.559 0.000 -6.486 -4.203
## ==============================================================================
## Omnibus: 2.988 Durbin-Watson: 1.252
## Prob(Omnibus): 0.225 Jarque-Bera (JB): 2.399
## Skew: 0.668 Prob(JB): 0.301
## Kurtosis: 2.877 Cond. No. 12.7
## ==============================================================================
##
## Warnings:
## [1] Standard Errors assume that the covariance matrix of the errors is correctly specified.R
También se mostrarán sólo las funciones básicas y será lo prioritario durante las prácticas.
modelinR = lm('mpg ~ wt', data = mtcars)
print(summary(modelinR))##
## Call:
## lm(formula = "mpg ~ wt", data = mtcars)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.543 -2.365 -0.125 1.410 6.873
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 37.285 1.878 19.86 < 2e-16 ***
## wt -5.344 0.559 -9.56 1.3e-10 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 3 on 30 degrees of freedom
## Multiple R-squared: 0.753, Adjusted R-squared: 0.745
## F-statistic: 91.4 on 1 and 30 DF, p-value: 1.29e-10En cualquier caso, el objetivo principal es interpretar las salidas.
¿Y si la variable \(Y\) no es continúa o no tiene distribución normal?
En regresión lineal simple y múltiple se asume que la variable \(Y\) sigue una distribución normal condicional en los valores de las variables explicativas \(X_1, ..., X_p\). En particular, se modela lo siguiente
\[E(Y|X_1,..., X_p)= \mathbf{\beta}\mathbf{X}\]
La extensión de este modelo implica considerar que la variable \(Y\) puede venir de cualquiera de las distribuciones que pertenecen a la familia exponencial. Por ejemplo
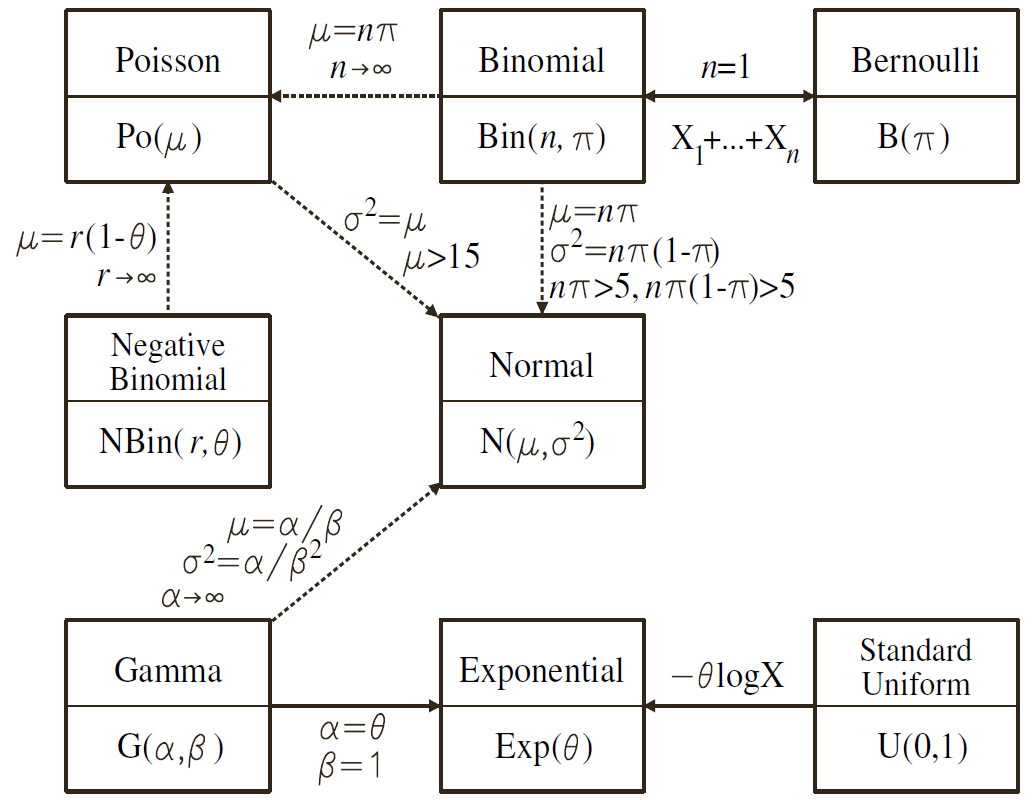
Además, ahora se modela para cada distribución lo siguiente:
\[g(E(Y|X_1,..., X_p))= \mathbf{\beta}\mathbf{X}.\]
Por ejemplo, para la regresión logística, donde \(Y|X_1,...,Xp\) es una \(Bernoulli(\pi)\)
\[log(\dfrac{\pi}{1-\pi})= \mathbf{\beta}\mathbf{X}.\]
En el curso analizaremos datos considerando los modelos lineales generalizados.