Tarea 1. Regresión lineal simple
Gonzalo Pérez, Dioney Rosas y Jonnathan Gutiérrez
6 de marzo de 2020
Tarea 1. Precede a examen 1. La tarea se deberá entregar el 17 de marzo. Se puede entregar por equipos de máximo 2 integrantes. Fecha de examen: 24 de marzo.
Usar una confianza de 95% o una significancia de .05 en los casos en donde no se requiera otro nivel de forma explícita.
1. Regresión a través del origen.
Ocasionalmente, un modelo en donde el valor del intercepto es conocido a priori y es igual a cero puede ser apropiado. Este modelo está dado por:
\[y_{i}=\beta x_{i}+\epsilon_{i}, \qquad i=1,...,n,\]
donde \(E(\epsilon_i)=0, \; V(\epsilon_i)=\sigma^2 \;\; \text{y} \;\; Cov(\epsilon_i, \epsilon_j)=0 \; \forall \; i\neq j; \; \; i,j = 1,...,n.\)
Muestre que el estimador de \(\beta\) obtenido por el método de mínimos cuadrados está dado por \(\widehat{\beta}=\sum_{i=1}^n x_{i}y_{i}\ / \sum_{i=1}^n x_{i}^2\). Argumente que \(\widehat{\beta}\) es un estimador lineal con respecto a las observaciones \(y_i\)’s.
Muestre que \(\widehat{\beta}\) es insesgado y que \(V(\widehat{\beta})=\sigma^2\ / \sum_{i=1}^n x_{i}^2\).
Considere además que \[y_i \sim N(\mu_i, \sigma^2),\] donde \(\mu_i=\beta x_i\) y con \(y_i\) y \(y_j\) variables aleatorias independientes para \(\; i\neq j\). Verifique que el estimador encontrado en i) también se obtiene usando máxima verosimilitud. Además, indique cual es el estimador máximo verosímil de \(\sigma^2\).
2.
Demuestre que bajo el modelo de regresión \[y_i=\alpha + \beta x_i + \epsilon_i,\]
donde \(E(\epsilon_i)=0, \; V(\epsilon_i)=\sigma^2 \;\; \text{y} \;\; Cov(\epsilon_i, \epsilon_j)=0 \; \forall \; i\neq j; \; \; i,j = 1,...,n\):
- los estimadores obtenidos por mínimos cuadrados \(\widehat{\alpha}\) y \(\widehat{\beta}\) tienen correlación \[corr(\widehat{\alpha},\widehat{\beta} )=-\sqrt{n}\dfrac{\bar{x}}{(\sum_{i=1}^{n}x_i^2)^{1/2}}.\]
- \[cov(\bar{y},\widehat{\beta} )=0.\]
3. Teorema Gauss-Markov
Bajo el modelo de regresión lineal simple: \[y_i=\alpha + \beta x_i + \epsilon_i,\]
donde \(E(\epsilon_i)=0, \; V(\epsilon_i)=\sigma^2 \;\; \text{y} \;\; Cov(\epsilon_i, \epsilon_j)=0 \; \forall \; i\neq j; \; \; i,j = 1,...,n\).
Demuestre que el estimador de mínimos cuadrados \(\widehat{\beta}\) satisface:
- es un estimador lineal e insesgado de \(\beta\) y
- su varianza es mínima dentro del conjunto de estimadores lineales insesgados de \(\beta\).
Nota: Para este ejercicio no usar la versión general del Teorema de Gauss Markov demostrado en clase. Recuerde que \(\widehat{\beta}=\dfrac{\sum_{i=1}^{n}(x_i-\overline{x})y_i}{\sum_{j=1}^{n}(x_j-\overline{x})^2}\).
4. Transformación de la variable explicativa
Considere el modelo de regresión lineal simple \(y_i=\alpha + \beta x_i + \epsilon_i\). Ahora suponga que cada \(x_i\) es reemplazada por \(cx_i\), donde \(c\neq 0\), es decir, \(x_i^*=cx_i\); y que se considera el modelo \(y_i=\alpha^* + \beta^* x_i^* + \epsilon_i^*\). Indique como se relacionan los siguientes estimadores y estadísticas, por ejemplo, si son iguales o si difieren y cómo:
- \(\widehat{\beta}\) y \(\widehat{\beta}^*\)
- \(\widehat{\alpha}\) y \(\widehat{\alpha}^*\)
- \(\widehat{\sigma}^2\) y \(\widehat{\sigma}^{*2}\)
- \(R^2\) y \(R^{*2}\)
- La estadística de prueba \(t\) para la prueba \(H_0:\beta =0\) vs \(H_a:\beta \neq 0\) y la correspondiente a la prueba \(H_0:\beta^* =0\) vs \(H_a:\beta^* \neq 0\).
Relación con el coeficiente de correlación de Pearson entre las variables \(X\) y \(Y\).
Para las preguntas 5 a 7, considere el modelo de regresión \[y_i=\alpha + \beta x_i + \epsilon_i,\]
donde \(E(\epsilon_i)=0, \; V(\epsilon_i)=\sigma^2 \;\; \text{y} \;\; Cov(\epsilon_i, \epsilon_j)=0 \; \forall \; i\neq j; \; \; i,j = 1,...,n\)
Además, que el coeficiente de determinación \(R^2\) y de correlación lineal de Pearson entre \(x\) y \(y\), \(r_{xy}\), se definen como \[ R^2 = \dfrac{\sum_{i=1}^{n}(\widehat{y}_i-\overline{y})^2}{\sum_{i=1}^{n}(y_i-\overline{y})^2} \qquad y \qquad r_{xy}=\dfrac{\sum_{i=1}^{n}(x_i-\overline{x})(y_i-\overline{y})}{(\sum_{i=1}^{n}(x_i-\overline{x})^2\sum_{i=1}^{n}(y_i-\overline{y})^2)^{1/2}}.\]
5.
Demuestre que \(R^2=r_{xy}^2\)
6.
Suponga que \(x_1\) y \(x_2\) son dos variables para las cuales se tienen observaciones: \(x_{11},....,x_{1n}\) y \(x_{21},....,x_{2n}\), respectivamente. Suponga que se ajusta el modelo de regresión \[ x_1=\alpha + \beta x_2 + \epsilon\] obteniendose los estimadores por mínimos cuadrados \(\widehat{\alpha}\) y \(\widehat{\beta}\), respectivamente. Ahora suponga que se ajusta el modelo \[ x_2=\alpha^* + \beta^*x_1 + \epsilon^* \] obteniendose los estimadores \(\widehat{\alpha}^*\) y \(\widehat{\beta}^*.\) Muestre que si \(r\) es el coeficiente de correlación lineal de Pearson entre \(x_1\) y \(x_2\), entonces \[r^2 = \widehat{\beta}^* \widehat{\beta}.\]
7.
Suponiendo que \(x\) y \(y\) son variables que siguen una distribución normal bivariada con coeficiente de correlación \(\rho=\rho_{xy}\), la prueba de hipótesis
\[``H_{0}:\rho=0 \quad vs \quad H_{a}:\rho \neq 0"\]
es de interés, pues en caso de rechazar \(H_0\) se puede decir que \(x\) y \(y\) no son independientes. Para realizar esta prueba se usa la siguiente estadística:
\[t^*=\frac{r\sqrt{n-2}}{\sqrt{1-r^2}},\]
donde \(r\) denota la correlación lineal de Pearson \(r_{xy}\). Se puede verificar que esta estadística sigue una distribución \(t_{n-2}\) bajo \(H_0\).
Demuestre \[\hat{\beta}=\Bigg[ \frac{\sum(y_{i}-\bar{y})^2}{\sum(x_{i}-\bar{x})^2}\Bigg]^{1/2} \times r.\]
Demuestre que \(t^*=t\), donde \(t\) es la estadística usada para realizar la prueba \[``H_{0}: \beta=0 \quad vs \quad H_{1}:\beta\neq 0 ",\] es decir, \[t=\frac{\widehat{\beta}}{\sqrt{\frac{\widehat{\sigma}^2}{\sum_{i=1}^n(x_i-\overline{x})^2}}}\]
8.
Una substancia usada en investigación médica es transportada en aviones de carga en paquetes de 1,000 ampolletas. Los datos que se muestran abajo corresponden a 10 envíos. En estos se reportan el número de veces que el paquete es transferido de un avión a otro en la ruta de envío \(x\), y el número de ampolletas encontradas rotas al llegar a su destino \(y\). Suponga que el modelo de regresión lineal simple es apropiado, \(y_i=\alpha + \beta x_i + \epsilon_i\).
i=c(1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10)
x=c(1 , 0 , 2 , 0 , 3 , 1 , 0 , 1 , 2 , 0)
y=c(16 , 9 , 17 , 12 , 22 , 13 , 8 , 15 , 19 , 11)
Datos8=data.frame(cbind(i,x,y))
Datos8ggplot(data=Datos8, aes(x=x,y=y))+
geom_point(colour="black")+theme_classic()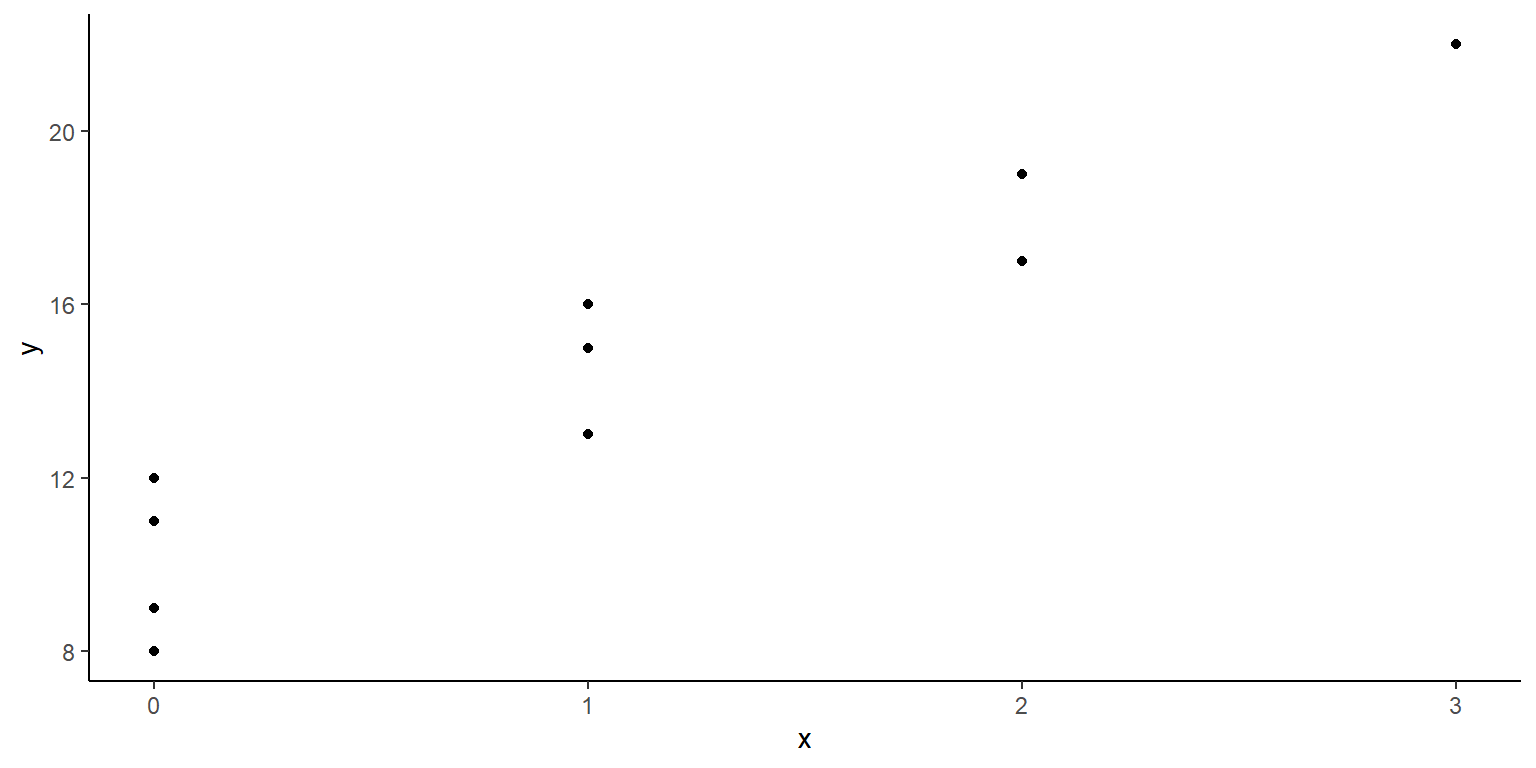
- Obtenga la función de regresión estimada. ¿La función de regresión lineal parece representar bien a las observaciones?
- Obtenga un estimador puntual del número esperado de ampolletas rotas cuando se hace una sola transferencia, \(x_{h}=1\).
- Estime el incremento en el número esperado de ampolletas rotas cuando se realizan dos transferencias en comparación con una.
- Estime \(\beta\) con un intervalo de confianza al \(95\%\). Inteprete.
- Realice una prueba de hipótesis para decidir si existe una relación lineal entre el número de veces que un paquete de ampolletas es transferido (Y) y el número de ampolletas rotas (X). Use un nivel de significancia de \(.05\).
- \(\alpha\) aquí representa el número medio de ampolletas rotas cuando no hay transferencias –i.e. cuando \(x_{h}=0.\) Obtenga un intervalo de confianza para \(\alpha\) e interprételo.
- Un consultor ha indicado, basado en experiencia previa, que el número medio de ampolletas rotas no excede \(9\) cuando no se hacen transferencias. Realice una prueba de hipótesis apropiada con una significancia de \(.025\) para comentar sobre lo indicado por el experto.
- Debido a cambios en las rutas de la aerolínea, los envíos podrían ser transferidos más frecuentemente que en el pasado. Se desea saber cual sería el número medio de ampolletas rotas si se hicieran cuatro transferencias, \(x_{h}=4.\) Use una confianza de \(99\%\) e interprete sus resultados.
- En el próximo envío habrá dos transferencias. Obtenga un intervalo para el número de ampolletas rotas en el embarque. Interprete sus resultados.
- En los días siguientes, se harán tres envíos independientes, en cada uno habrá dos transferencias. Obtenga un intervalo al \(99\%\) para el número medio de ampolletas rotas en los tres envíos. Convierta este intervalo en uno al \(99\%\) para el número total de ampolletas rotas en los tres envíos.
- Calcule \(R^2\). ¿Qué proporción de la variación en \(Y\) es explicada por la introducción de \(X\) en el modelo de regresión?
9.
Los \(ping\ddot{u}inos\) \(Macaroni\) ponen nidadas de dos huevos de tamaño diferente. El peso en gramos de los huevos de 11 nidadas se presenta en la tabla de abajo.
- Ajuste la recta de regresión del peso del huevo mayor en el peso del huevo menor. Comente sobre el ajuste del modelo.
- Pruebe si la pendiente de la regresión difiere significativamente (estadísticamente) de la unidad. Interprete.
- Posteriormente se observa el peso de los huevos de una nueva nidada, observándose un peso de 75 y 115 gramos. Usando un intervalo adecuado, comente sobre la sospecha de que la nidada de huevos no proviene de pinguinos \(Macaroni.\)
x=c(79, 93, 100, 105, 101, 96, 96, 109, 70, 71, 87)
y=c(133, 143, 164, 171, 165, 159, 162, 170, 127, 133, 148 )
Datos9=data.frame(cbind(x,y))
kable(Datos9)| x | y |
|---|---|
| 79 | 133 |
| 93 | 143 |
| 100 | 164 |
| 105 | 171 |
| 101 | 165 |
| 96 | 159 |
| 96 | 162 |
| 109 | 170 |
| 70 | 127 |
| 71 | 133 |
| 87 | 148 |
ggplot(data=Datos9, aes(x=x,y=y))+
geom_point(colour="black")+theme_classic()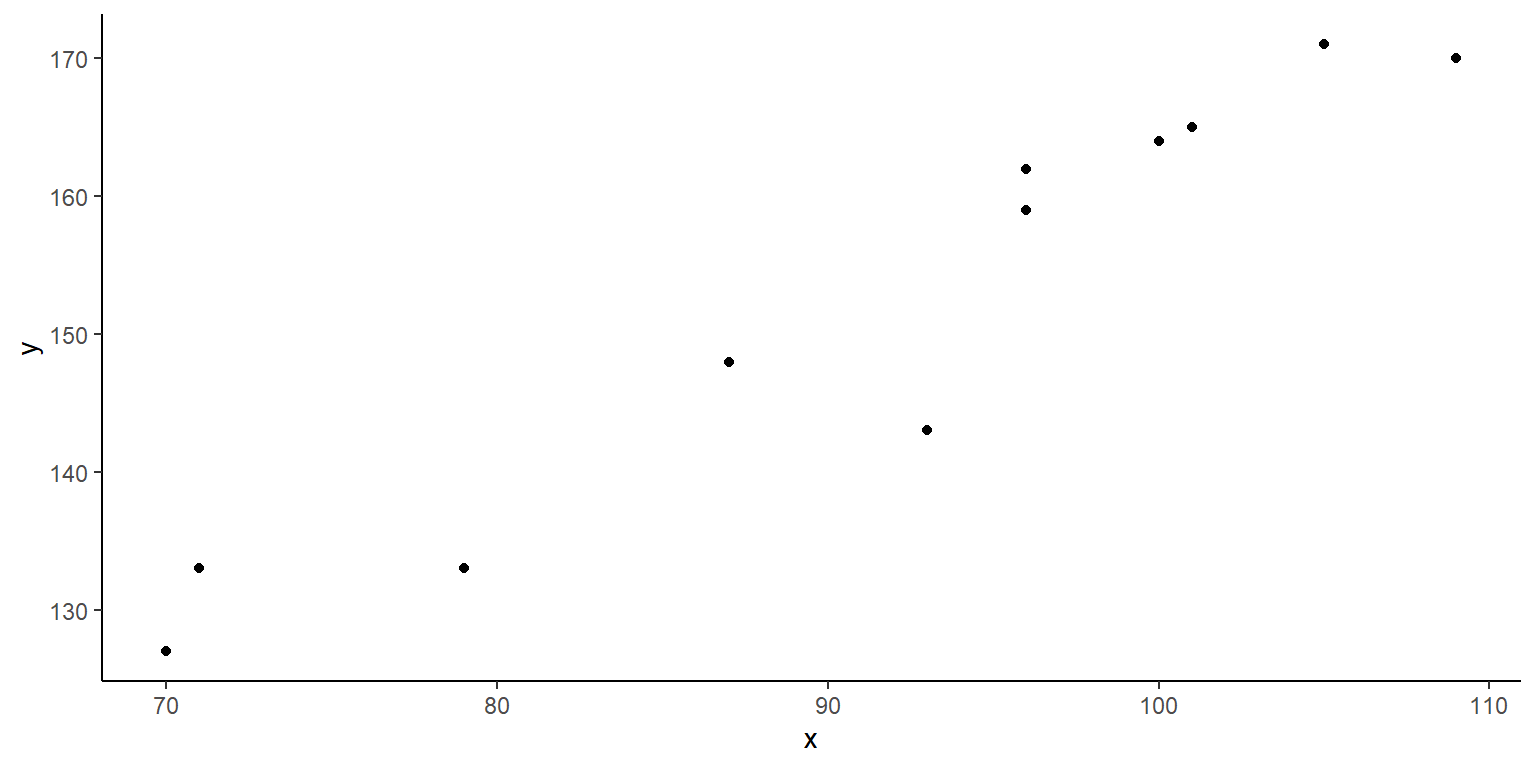
10.
En una gran universidad se seleccionó al azar a 7 estudiantes de economía y se les aplicó una encuesta. Dos de las preguntas fueron: (1) ¿Cuál es el porcentaje de GPA en el semestre anterior?, (2) En promedio ¿Cuántas horas a la semana pasó durante el último semestre en el bar X? El bar X es un lugar muy conocido por los estudiantes.
Est=c(1 , 2 , 3 , 4 , 5 , 6 , 7 )
G=c(3.6, 2.2, 3.1, 3.5, 2.7, 2.6, 3.9)
H=c(3, 15, 8, 9, 12, 12, 4)
Datos10=data.frame(cbind(Est,G,H))
Datos10ggplot(data=Datos10, aes(x=H,y=G))+
geom_point(colour="black")+theme_classic()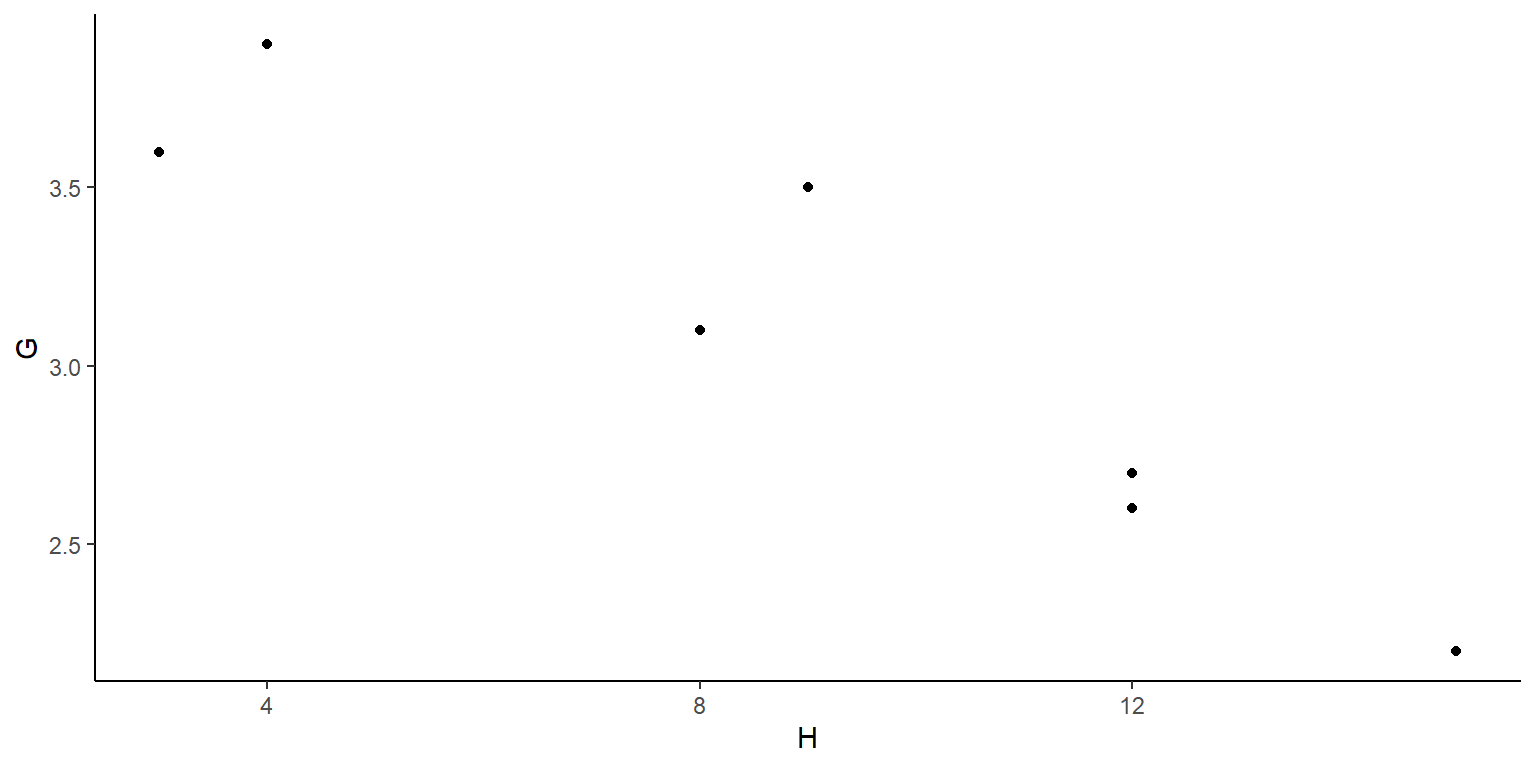
- ¿Dirías que un modelo lineal simple serviría para describir la relación entre G (puntaje del GPA) y H (horas a la semana en el bar)?
- Ajusta un modelo lineal simple
- Encuentra \(\hat{\sigma}^2\), las desviaciones estándar estimadas para \(\hat{\alpha}\) y \(\hat{\beta}\), sus intervalos de confianza y el \(R^2\). ¿Qué puedes decir al respecto?
- Realiza la prueba \(t\) para contrastar \(H_{0}: \beta=0 \quad vs \quad H_{a}:\beta \neq 0\). Comenta.
- Obtén la tabla ANOVA y realiza la prueba asociada con una significancia de .05.
- Suponga ahora que un nuevo estudiante de economía pasa 15 horas a la semana en el bar durante las dos primeras semanas de clase. Calcule un intervalo para su porcentaje de GPA en su primer semestre si continúa pasando 15 horas a la semana en el bar.
- ¿Cuál sería la variación promedio del porcentaje de GPA al aumentar en una hora a la semana la estancia en el bar? De un intervalo de confianza al \(90\%\)
- Suponga que un grupo de 5 estudiantes acudirá al bar en promedio 10 horas a la semana durante el siguiente semestre, ¿Cuál será el porcentaje de GPA promedio de los cinco estudiantes para el próximo semestre?. Calcule un intervalo.
- Describa en general cuál es el porcentaje de GPA promedio de los estudiantes que asisten 8 horas a la semana al bar.
- Suponga que al lado del bar X existe una cafeteria. Un analista supone que, en principio, el porcentaje promedio de GPA de los estudiantes que no acuden al bar es igual al porcentaje promedio de los que no acuden a la cafetería. Sin embargo, cree por su experiencia que el patrón observado en el cambio promedio del porcentaje de GPA al aumentar una hora de estancia en la cafetería es sólo de la mitad de la observada al aumentar una hora de estancia en el bar. Es decir, al analista le parece plausible usar un modelo de regresión del estilo: \[y_{i}=\alpha+\frac{\beta}{2} x_{i}^*+\epsilon\] Donde \(x^*\) es el promedio en horas a la semana que los estudiantes pasan en la cafetería durante un semestre y \(y\) el correspondiente porcentaje de GPA. Los demás parámetros asociados a este modelo son los mismos a los asociados al modelo original. Dado que no se cuentan con observaciones para este estudio particular y sólo se tiene el supuesto del analista, se deciden usar los estimadores \(\hat{\alpha}\) y \(\hat{\beta}\). Calcule un intervalo de confianza al \(95\%\) para el porcentaje de GPA promedio de los estudiantes que acuden 8 horas a la semana al cafetería.